
【题目】在平面直角坐标系中,直线l过点P(2, ![]() )且倾斜角为α,以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=4cos(θ﹣
)且倾斜角为α,以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=4cos(θ﹣ ![]() ),直线l与曲线C相交于A,B两点;
),直线l与曲线C相交于A,B两点;
(1)求曲线C的直角坐标方程;
(2)若 ![]() ,求直线l的倾斜角α的值.
,求直线l的倾斜角α的值.
科目:高中数学 来源: 题型:
【题目】过抛物线y2=2px(p>0)的焦点F的直线l与抛物线交于B,C两点,l与抛物线的准线交于点A,且|AF|=6,![]() =2
=2![]() ,
,
(1)求抛物线方程.
(2)求|BC|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的单调函数,且对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=3,则方程f(x)﹣f′(x)=2的解所在的区间是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(1,2)
D.(2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )ax , a为常数,且函数的图象过点(﹣1,2).
)ax , a为常数,且函数的图象过点(﹣1,2).
(1)求a的值;
(2)若g(x)=4﹣x﹣2,且g(x)=f(x),求满足条件的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(Ⅰ)证明:平面ACD⊥平面ABC;
(Ⅱ)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D﹣AE﹣C的余弦值.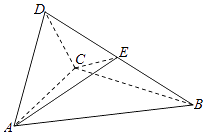
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在(0,+∞)上的函数f(x)满足xf′(x)﹣f(x)=xlnx,f( ![]() )=
)= ![]() ,则f(x)( )
,则f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值,又有极小值
D.既无极大值,也无极小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com