
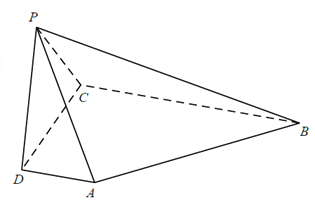
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)![]() .(Ⅱ)见解析;(Ⅲ)
.(Ⅱ)见解析;(Ⅲ)![]() .
.
【解析】试题分析:本小题主要考查两条异面直线所成的角、直线与平面垂直、直线与平面所成的角等基础知识.求两条异面直线所成的角,首先要借助平行线找出异面直线所成的角,然后借助解三角形求出角,证明线面垂直只需寻求线线垂直,求线面角首先利用转化思想寻求直线与平面所成的角,本题作![]() 是一步重要的转化,寻求斜线、垂线,斜足、垂足、斜线在平面内的射影,找到线面角后利用三角形边角关系求出线面角.求线面角也可转化为点到平面的距离“盲求”.
是一步重要的转化,寻求斜线、垂线,斜足、垂足、斜线在平面内的射影,找到线面角后利用三角形边角关系求出线面角.求线面角也可转化为点到平面的距离“盲求”.
考查空间想象能力、运算求解能力和推理论证能力.
试题解析:(Ⅰ)如图,由已知AD//BC,学|科网故![]() 或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC,所以AD⊥PD.在Rt△PDA中,由已知,得
或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC,所以AD⊥PD.在Rt△PDA中,由已知,得![]() ,故
,故![]() .
.
所以,异面直线AP与BC所成角的余弦值为![]() .
.
(Ⅱ)证明:因为AD⊥平面PDC,直线PD![]() 平面PDC,所以AD⊥PD.又因为BC//AD,所以PD⊥BC,又PD⊥PB,所以PD⊥平面PBC.
平面PDC,所以AD⊥PD.又因为BC//AD,所以PD⊥BC,又PD⊥PB,所以PD⊥平面PBC.
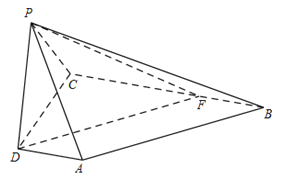
(Ⅲ)解:过点D作AB的平行线交BC于点F,连结PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角.
因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,所以![]() 为直线DF和平面PBC所成的角.
为直线DF和平面PBC所成的角.
由于AD//BC,DF//AB,故BF=AD=1,由已知,得CF=BC–BF=2.又AD⊥DC,故BC⊥DC,在Rt△DCF中,可得![]() ,在Rt△DPF中,可得
,在Rt△DPF中,可得![]() .
.
所以,直线AB与平面PBC所成角的正弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】汽车租赁公司为了调查A,B两种车型的出租情况,现随机抽取了这两种车型各100辆汽车,分别统计了每辆车某个星期内的出租天数,统计数据如下表: A型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
B型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
( I)从出租天数为3天的汽车(仅限A,B两种车型)中随机抽取一辆,估计这辆汽车恰好是A型车的概率;
(Ⅱ)根据这个星期的统计数据,估计该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率;
(Ⅲ)如果两种车型每辆车每天出租获得的利润相同,该公司需要从A,B两种车型中购买一辆,请你根据所学的统计知识,给出建议应该购买哪一种车型,并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A (1,2),B(a,1),C(2,3),D(﹣1,b)(a,b∈R)是复平面上的四个点,且向量 ![]() ,
, ![]() 对应的复数分别为z1 , z2 . (Ⅰ)若z1+z2=1+i,求z1 , z2
对应的复数分别为z1 , z2 . (Ⅰ)若z1+z2=1+i,求z1 , z2
(Ⅱ)若|z1+z2|=2,z1﹣z2为实数,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2. (Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() )﹣cos2x.
)﹣cos2x.
(1)求f(x)的最小正周期及x∈[ ![]() ,
, ![]() ]时f(x)的值域;
]时f(x)的值域;
(2)在△ABC中,角A、B、C所对的边为a,b,c,且角C为锐角,S△ABC= ![]() ,c=2,f(C+
,c=2,f(C+ ![]() )=
)= ![]() ﹣
﹣ ![]() .求a,b的值.
.求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() ,g(x)=2x+a,若x1∈[
,g(x)=2x+a,若x1∈[ ![]() ,3],x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是( )
,3],x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是( )
A.a≤1
B.a≥1
C.a≤0
D.a≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣lnx;g(x)= ![]() .
.
(1)讨论函数f(x)的单调性;
(2)求证:若a=e(e是自然常数),当x∈[1,e]时,f(x)≥e﹣g(x)恒成立;
(3)若h(x)=x2[1+g(x)],当a>1时,对于x1∈[1,e],x0∈[1,e],使f(x1)=h(x0),求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com