
【题目】已知函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
![]() 若
若![]() ,求函数
,求函数![]() 的极值;
的极值;
![]() 若关于
若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围。
的取值范围。
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图,已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4第一小组的频数是5.
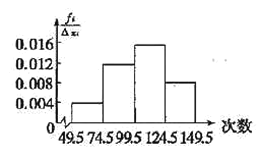
(1)求第四小组的频率和该组参加这次测试的学生人数;
(2)在这次测试中,学生跳绳次数的中位效落在第几小组内?
(3)从第一小组中选出2人,第三小组中选出3人组成队伍代表学校参加区里的小学生体质测试,在测试的某一环节,需要从这5人中任选两人参加测试,求这两人来自同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四色猜想是世界三大数学猜想之一,1976年美国数学家阿佩尔与哈肯证明了四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用1,2,3,4四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为1,粗实线围成的各区域(如区域D由两个边长为1的小正方形构成)上分别标有数字1,2,3,4的四色地图符合四色定理,区域A、B、C、D、E、F标记的数字丢失若在该四色地图上随机取一点,则恰好取在标记为4的区域的概率是
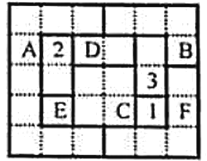
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣bx+lnx,(a,b∈R).
(1)若a=1,b=3,求函数f(x)的单调增区间;
(2)若b=0时,不等式f(x)≤0在[1,+∞)上恒成立,求实数a的取值范围;
(3)当a=1,b>![]() 时,记函数f(x)的导函数f
时,记函数f(x)的导函数f![]() (x)的两个零点是x1和x2(x1<x2),求证:f(x1)﹣f(x2)>
(x)的两个零点是x1和x2(x1<x2),求证:f(x1)﹣f(x2)>![]() ﹣3ln2.
﹣3ln2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com