
已知向量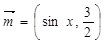 ,
,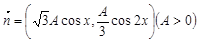 ,函数
,函数 的最大值为6.
的最大值为6.
(Ⅰ)求 ;
;
(Ⅱ)将函数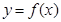 的图象向左平移
的图象向左平移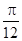 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的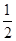 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数 的图象.求
的图象.求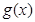 在
在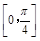 上的值域.
上的值域.
(Ⅰ)A=6;(Ⅱ)g(x)在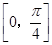 上的值域为.
上的值域为.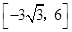
解析试题分析:(Ⅰ)由向量的数量积的定义得: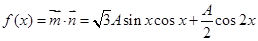 ,然后降次化一得:
,然后降次化一得: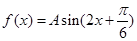 ,由此得A=6.
,由此得A=6.
(Ⅱ)因为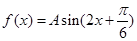 ,所以将函数
,所以将函数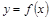 的图象向左平移
的图象向左平移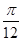 个单位后得到y=6sin
个单位后得到y=6sin =6sin
=6sin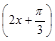 的图象;再将得到图象上各点横坐标缩短为原来的
的图象;再将得到图象上各点横坐标缩短为原来的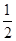 倍,
倍,
纵坐标不变,得到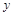 =6sin
=6sin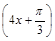 的图象.即g(x)=6sin
的图象.即g(x)=6sin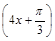 .因为x∈
.因为x∈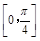 ,所以4x+
,所以4x+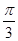 ∈
∈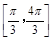 .故g(x)在
.故g(x)在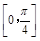 上的值域为
上的值域为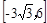 .
.
试题解析:(Ⅰ)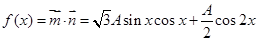 .2分
.2分
=A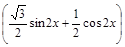 =Asin
=Asin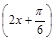 ..4分
..4分
因为A>0,由题意知,A=6. .6分
(Ⅱ)由(Ⅰ)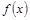 =6sin
=6sin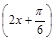 .将函数
.将函数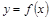 的图象向左平移
的图象向左平移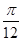 个单位后得到y=
个单位后得到y=
6sin =6sin
=6sin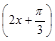 的图象;再将得到图象上各点横坐标缩短为原来的
的图象;再将得到图象上各点横坐标缩短为原来的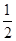 倍,
倍,
纵坐标不变,得到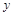 =6sin
=6sin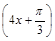 的图象。 8分
的图象。 8分
因此,g(x)=6sin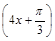 .因为x∈
.因为x∈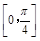 ,所以4x+
,所以4x+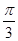 ∈
∈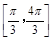 .
.
故g(x)在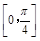 上的值域为
上的值域为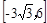 . .12分
. .12分
考点:三角变换及三角函数的值域.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com