
【题目】为了检验两种不同的课堂教学模式对学生的成绩是否有影响,现从高二年级的甲(实行的“问题——探究式”)、乙(实行的“自学——指导式”)两个班中每班任意抽取20名学生进行测试,他们的成绩(总分150分)分布茎叶图如图所示(以十位百位为茎,个位为叶):

(1)若从参与测试的学生试卷中挑选2份卷面分数为90~100分的试着进行卷面分析,求抽取的2份试卷恰好每班1份的概率?
(2)记成绩在120分以上(包括120分)为优秀,其他的成绩为一般,请完成下面![]() 列联表,并分析是否有足够的把握(90%以上)认为这两种课堂教学模式对学生的成绩有影响?
列联表,并分析是否有足够的把握(90%以上)认为这两种课堂教学模式对学生的成绩有影响?
成绩 班级 | 优秀人数 | 一般人数 | 总计 |
甲班 | |||
乙班 | |||
总计 |
附: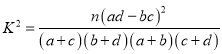
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)![]() ;(2)列联表见解析,没有足够的把握认为这两种课堂教学模式对学生成绩有影响
;(2)列联表见解析,没有足够的把握认为这两种课堂教学模式对学生成绩有影响
【解析】
(1)本题是一个等可能事件的概率,将所有的基本事件一一列举出来,从中找出事件“抽取的2份试卷恰好每班1份”所包含的基本事件,用概率公式即可求解;
(2)根据所给的数据,填写![]() 列联表,并据此求出观测值,与临界值表相对应,得到结论.
列联表,并据此求出观测值,与临界值表相对应,得到结论.
(1)从茎叶图上可知,90~100分的试卷共有5份,其中甲班3份,
乙班2份,记甲班的试卷为![]() ,
,![]() ,
,![]() ,乙班的试卷为
,乙班的试卷为![]() ,
,![]() ,
,
现从中抽取2份,共有以下情况:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() 共10种,
共10种,
其中每班1份情况有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6种,
共6种,
记“抽取的2份试卷恰好每班1份”为事件![]() ,
,
则![]() .
.
(2)
成绩 班级 | 优秀人数 | 一般人数 | 总计 |
甲班 | 10 | 10 | 20 |
乙班 | 11 | 9 | 20 |
总计 | 21 | 19 | 40 |
![]()
故没有足够的把握认为这两种课堂教学模式对学生成绩有影响.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学文化的优秀遗产,数学家刘徽在注解《九章算术》时,发现当圆内接正多边行的边数无限增加时,多边形的面积可无限逼近圆的面积,为此他创立了割圆术,利用割圆术,刘徽得到了圆周率精确到小数点后四位3.1416,后人称3.14为徽率,如图是利用刘徽的割圆术设计的程序框图,若结束程序时,则输出的![]() 为( )(
为( )(![]() ,
,![]() ,
,![]() )
)

A. 6 B. 12 C. 24 D. 48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:![]() ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.
(1)现从年龄在![]() 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用![]() 表示年龄在
表示年龄在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() .当
.当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感市旅游局为了了解双峰山景点在大众中的熟知度,从年龄在15~65岁的人群中随机抽取n人进行问卷调查,把这n人按年龄分成5组:第一组[15,25),第二组[25,35),第三组[35,45),第四组[45,55),第五组[55,65],得到的样本的频率分布直方图如右:

调查问题是“双峰山国家森林公园是几A级旅游景点?”每组中回答正确的人数及回答正确的人数占本组的频率的统计结果如下表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | y | 0.9 |
第4组 | [45,55) | 9 | a |
第5组 | [55,65] | 7 | b |
(1)分别求出n,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人;
(3)在(2)抽取的6人中随机抽取2人,求所抽取的两人来自不同年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)![]() ,函数g(θ)=cos2θ+2sinθ
,函数g(θ)=cos2θ+2sinθ![]() ,θ∈[m,
,θ∈[m,![]() ].m,b∈R.
].m,b∈R.
(1)求b的值;
(2)判断函数f(x)在[0,1]上的单调性,并证明;
(3)当x∈[0,1]时,函数g(θ)的最小值恰为f(x)的最大值,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从学生文艺部6名成员(4男2女)中,挑选2人参加学校举办的文艺汇演活动.
(1)求男生甲被选中的概率;
(2)在已知男生甲被选中的条件下,女生乙被选中的概率;
(3)在要求被选中的两人中必须一男一女的条件下,求女生乙被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
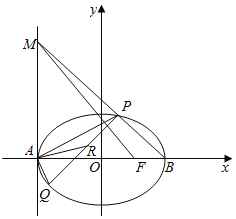
【题目】已知椭圆C:![]() 的左右顶点为A、B,右焦点为F,一条准线方程是
的左右顶点为A、B,右焦点为F,一条准线方程是![]() ,短轴一端点与两焦点构成等边三角形,点P、Q为椭圆C上异于A、B的两点,点R为PQ的中点
,短轴一端点与两焦点构成等边三角形,点P、Q为椭圆C上异于A、B的两点,点R为PQ的中点
![]() 求椭圆C的标准方程;
求椭圆C的标准方程;
![]() 直线PB交直线
直线PB交直线![]() 于点M,记直线PA的斜率为
于点M,记直线PA的斜率为![]() ,直线FM的斜率为
,直线FM的斜率为![]() ,求证:
,求证:![]() 为定值;
为定值;
![]() 若
若![]() ,求直线AR的斜率的取值范围.
,求直线AR的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学的对称美在中国传统文化中多有体现,譬如如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的和谐美.如果能够将圆的周长和面积同时平分的函数称为这个圆的“优美函数”,下列说法正确的是( )

A.对于任意一个圆,其“优美函数”有无数个
B.![]() 可以是某个圆的“优美函数”
可以是某个圆的“优美函数”
C.正弦函数![]() 可以同时是无数个圆的“优美函数”
可以同时是无数个圆的“优美函数”
D.函数![]() 是“优美函数”的充要条件为函数
是“优美函数”的充要条件为函数![]() 的图象是中心对称图形
的图象是中心对称图形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com