
(-∞,-2)∪(3,+∞) 12π
分析:A,可设极点为O,则∠AOB=

,而|OA|=3,|OB|=4,由余弦定理即可求得AB两点间的距离;
B,可构造函数f(x)=|x+1|+|x-2|=
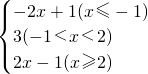
,由f(x)>5即可求得其解集;
C,由正弦定理
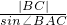
=2R(R为圆O的半径)即可求得R,从而可得圆O的面积.
解答:A:设极点为O,∵在极坐标系中,两点为
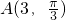
,
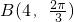
,
∴∠AOB=

,又|OA|=3,|OB|=4,
∴|AB|
2=|OA|
2+|OB|
2-2|OA|•|OB|cos∠AOB=9+16-2×3×4×

=13,
∴|AB|=

;
B:令f(x)=|x+1|+|x-2|,则f(x)=
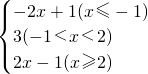
,
∵|x+1|+|x-2|>5,
∴当x≤-1,-2x+1>5,解得x<-2
当-1<x<2,有3>5(舍去)
当x≥2,2x-1>5解得x>3.
综上所述,f(x)>5的解集为{x|x<-2或x>3};
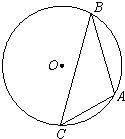
C:在△ABC中,设△ABC中的外接圆的半径为R,面积为S,
∵BC=6,∠BAC=120°,
∴由正弦定理得:
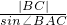
=2R,即
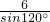
=4

=2R,
∴R=2

,
∴S=πR
2=12π.
故A的答案为:

;B的答案为:{x|x<-2或x>3};C的答案为:12π.
点评:本题A考查简单曲线的极坐标方程,B考查绝对值不等式,C考查正弦定理,着重考查正弦定理与余弦定理的应用及绝对值不等式的解法,属于基础题.

 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)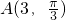 ,
,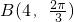 间的距离是________.
间的距离是________. (-∞,-2)∪(3,+∞) 12π
(-∞,-2)∪(3,+∞) 12π ,而|OA|=3,|OB|=4,由余弦定理即可求得AB两点间的距离;
,而|OA|=3,|OB|=4,由余弦定理即可求得AB两点间的距离;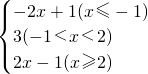 ,由f(x)>5即可求得其解集;
,由f(x)>5即可求得其解集;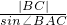 =2R(R为圆O的半径)即可求得R,从而可得圆O的面积.
=2R(R为圆O的半径)即可求得R,从而可得圆O的面积.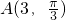 ,
,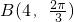 ,
, ,又|OA|=3,|OB|=4,
,又|OA|=3,|OB|=4, =13,
=13, ;
;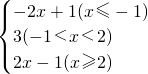 ,
,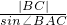 =2R,即
=2R,即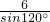 =4
=4 =2R,
=2R, ,
, ;B的答案为:{x|x<-2或x>3};C的答案为:12π.
;B的答案为:{x|x<-2或x>3};C的答案为:12π.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)