
【题目】如图,已知点H在正方体![]() 的对角线
的对角线![]() 上,∠HDA=
上,∠HDA=![]() .
.

(1)求DH与![]() 所成角的大小;
所成角的大小;
(2)求DH与平面![]() 所成角的正弦值.
所成角的正弦值.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】两县城![]() 和
和![]() 相距
相距![]() ,现计划在两县城外位于线段
,现计划在两县城外位于线段![]() 上选择一点
上选择一点![]() 建造一个两县城的公共垃圾处理厂,已知垃圾处理厂对城市的影响度与所选地点到城市的的距离关系最大,其他因素影响较小暂时不考虑,垃圾处理厂对城
建造一个两县城的公共垃圾处理厂,已知垃圾处理厂对城市的影响度与所选地点到城市的的距离关系最大,其他因素影响较小暂时不考虑,垃圾处理厂对城![]() 和城
和城![]() 的总影响度为对城
的总影响度为对城![]() 与城
与城![]() 的影响度之和. 记
的影响度之和. 记![]() 点到城
点到城![]() 的距离为
的距离为![]() ,建在
,建在![]() 处的垃圾处理厂对城
处的垃圾处理厂对城![]() 和城
和城![]() 的总影响度为
的总影响度为![]() ,统计调查表明:垃圾处理厂对城
,统计调查表明:垃圾处理厂对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数2.7;垃圾处理厂对城
的距离的平方成反比,比例系数2.7;垃圾处理厂对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为
的距离的平方成反比,比例系数为![]() ;且当垃圾处理厂
;且当垃圾处理厂![]() 与城
与城![]() 距离为
距离为![]() 时对城
时对城![]() 和城
和城![]() 的总影响度为0.029.
的总影响度为0.029.
(1) 将![]() 表示成
表示成![]() 的函数;
的函数;
(2) 讨论⑴中函数的单调性,并判断在线段![]() 上是否存在一点,使建在此处的垃圾处理厂对城
上是否存在一点,使建在此处的垃圾处理厂对城![]() 和城
和城![]() 的总影响度最小?若存在,求出该点到城
的总影响度最小?若存在,求出该点到城![]() 的距离;若不存在,说明理由.
的距离;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取![]() 个,利用水果的等级分类标准得到的数据如下:
个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)若将频率视为概率,从这![]() 个水果中有放回地随机抽取
个水果中有放回地随机抽取![]() 个,求恰好有
个,求恰好有![]() 个水果是礼品果的概率;(结果用分数表示)
个水果是礼品果的概率;(结果用分数表示)
(2)用分层抽样的方法从这![]() 个水果中抽取
个水果中抽取![]() 个,再从抽取的
个,再从抽取的![]() 个水果中随机抽取
个水果中随机抽取![]() 个,
个,![]() 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】麻团又叫煎堆,呈球形,华北地区称麻团,是一种古老的中华传统特色油炸面食,寓意团圆。制作时以糯米粉团炸起,加上芝麻而制成,有些包麻茸、豆沙等馅料,有些没有。一个长方体形状的纸盒中恰好放入4个球形的麻团,它们彼此相切,同时与长方体纸盒上下底和侧面均相切,其俯视图如图所示,若长方体纸盒的表面积为576 ![]() ,则一个麻团的体积为_______
,则一个麻团的体积为_______![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】M是椭圆T:![]() 1(a>b>0)上任意一点,F是椭圆T的右焦点,A为左顶点,B为上顶点,O为坐标原点,如下图所示,已知|MF|的最大值为3
1(a>b>0)上任意一点,F是椭圆T的右焦点,A为左顶点,B为上顶点,O为坐标原点,如下图所示,已知|MF|的最大值为3![]() ,且△MAF面积最大值为3
,且△MAF面积最大值为3![]() .
.
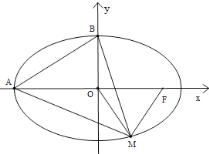
(1)求椭圆T的标准方程
(2)求△ABM的面积的最大值S0.若点N(x,y)满足x∈Z,y∈Z,称点N为格点.问椭圆T内部是否存在格点G,使得△ABG的面积S∈(6,S0)?若存在,求出G的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx![]() .
.
(1)若a=4,求函数f(x)的单调区间;
(2)若函数f(x)在区间(0,1]内单调递增,求实数a的取值范围;
(3)若x1、x2∈R+,且x1≤x2,求证:(lnx1﹣lnx2)(x1+2x2)≤3(x1﹣x2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆C:
中,已知椭圆C:![]() (
(![]() >
>![]() >0)的右焦点为F(1,0),且过点(1,
>0)的右焦点为F(1,0),且过点(1,![]() ),过点F且不与
),过点F且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆C交于A,B两点,点P在椭圆上,且满足
与椭圆C交于A,B两点,点P在椭圆上,且满足![]() .
.
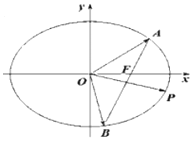
(1)求椭圆C的标准方程;
(2)若![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com