【题目】已知椭圆
:
的四个顶点恰好是一边长为2，一内角为
的菱形的四个顶点.
(1)求椭圆的方程；
(2)若直线
交椭圆于
两点，在直线
上存在点
,使得
为等边三角形,求
的值.
【答案】（1）
；（2）
或
．
【解析】
试题（1）求椭圆标准方程，要确定
的值，题中已知四个顶点形成的菱形是确定的，而椭圆的顶点为
，因此易得；（2）本小题采取解析几何的基本解法，
是等边三角形的条件是三边相等，或两内角为60°，或
且
，我们采用且，由线段
的中垂线与直线
相交求得点
的坐标，计算
，直线
与椭圆相交求得
点坐标，计算
，利用求得
值，由于涉及到的垂线．因此对按和
分类讨论．
试题解析：(1)因为椭圆
:
的四个顶点恰好是一边长为2，
一内角为
的菱形的四个顶点, 所以
,
椭圆的方程为
(2)设
,则
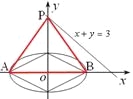
（i）当直线的斜率为0时，的垂直平分线就是
轴，轴与直线
的交点为
,
又
，
所以是等边三角形,所以满足条件；
(ii)当直线的斜率存在且不为0时，设的方程为
所以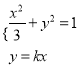
，化简得
解得
所以
又的中垂线为
，它的交点记为
由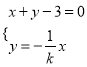
解得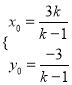
则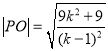
因为为等边三角形， 所以应有
代入得到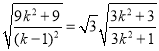
，解得（舍），
综上可知，或
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】如图，平面四边形ABCD中，E，F是AD，BD中点，
，
，将
沿对角线BD折起至
，使平面
平面BCD，则四面体
中，下列结论不正确的是（ ）
A.
平面
B.异面直线CD与
所成的角为
C.异面直线EF与
所成的角为
D.直线与平面BCD所成的角为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【选修4-4：坐标系与参数方程】
在平面直角坐标系
中，以坐标原点
为极点， 
轴的正半轴为极轴建立极坐标系．已知曲线
的极坐标方程为
．倾斜角为
，且经过定点
的直线
与曲线
交于
两点．
(Ⅰ)写出直线
的参数方程的标准形式，并求曲线
的直角坐标方程；
(Ⅱ)求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（
为自然对数的底数），
为
的导函数，且
.
（1）求实数
的值；
（2）若函数在
处的切线经过点
，求函数的极值；
（3）若关于
的不等式
对于任意的
恒成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝lg(x＋1)．
(1)若0<f(1－2x)－f(x)<1，求实数x的取值范围；
(2)若g(x)是以2为周期的偶函数，且当0≤x≤1时，有g(x)＝f(x)，当x∈[1,2]时，求函数y＝g(x)的解析式．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】等差数列
的前
项和为
，数列
满足：
，
，当
时，
，且，
，
成等比数列，
.
（1）求数列，的通项公式；
（2）求证：数列中的项都在数列中；
（3）将数列、
的项按照：当为奇数时，
放在前面：当为偶数时，
放在前面进行“交叉排列”，得到一个新的数列：
，
，
，
，
，
，…这个新数列的前和为
，试求的表达式.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为促进全面健身运动，某地跑步团体对本团内的跑友每周的跑步千米数进行统计，随机抽取的100名跑友，分别统计他们一周跑步的千米数，并绘制了如图频率分布直方图.
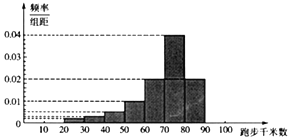
（1）由频率分布直方图计算跑步千米数不小于70千米的人数；
（2）已知跑步千米数在
的人数是跑步千米数在
的
，跑步千米数在
的人数是跑步千米数在
的
，现在从跑步千米数在
的跑友中抽取3名代表发言，用
表示所选的3人中跑步千米数在的人数，求的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一袋中有大小、形状相同的2个白球和10个黑球，从中任取一球．如果取出白球，则把它放回袋中；如果取出黑球，则该球不再放回，另补一个白球放到袋中．在重复
次这样的操作后，记袋中的白球个数为
．
（1）求
；
（2）设
，求
；
（3）证明：
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，AB、PA、PBC分别为⊙O的切线和割线，切点A是BD的中点，AC、BD相交于点E，AB、PE相交于点F，直线CF交⊙O于另一点G、交PA于点K.
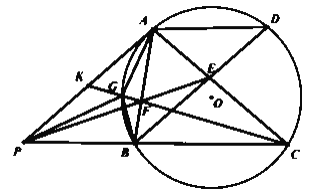
证明：（1）K是PA的中点；（2）
..
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com