试题分析:∵
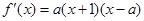
且

在
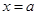
处取到极大值,则必有
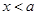
时,
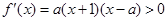
,且
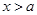
时,
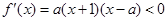
.当
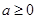
时,不成立;当
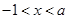
时,有
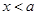
时,
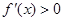
,
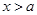
时,
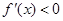
,符合题意;当
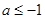
时,有
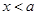
时,
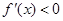
,
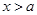
时,
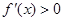
,

在
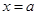
处取到极小值.综合可得
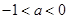
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
设函数
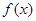
)是定义在(一
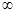
,0)上的可导函数,其导函数为
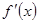
,且有
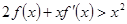
,则不等式
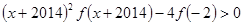
的解集为-------------
A,
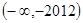
B.

C.
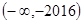
D.
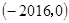
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知a≤
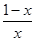
+ln x对任意x∈[
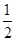
,2]恒成立,则a的最大值为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
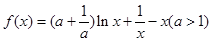
.
(1)讨论函数
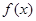
在
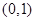
上的单调性;
(2)当
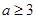
时,曲线
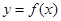
上总存在相异两点,
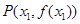
,
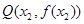
,使得
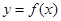
曲线在
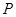
、
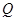
处的切线互相平行,求证:
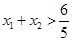
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
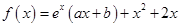
,曲线
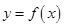
经过点
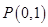
,
且在点
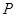
处的切线为
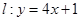
.
(1)求
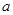
、
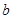
的值;
(2)若存在实数
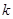
,使得
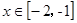
时,
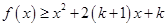
恒成立,求
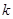
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
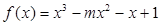
,其中
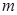
为实数.
(1)当
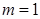
时,求函数
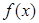
在区间
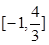
上的最大值和最小值;
(2)若对一切的实数
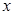
,有
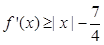
恒成立,其中
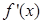
为
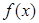
的导函数,求实数
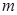
的取值范围.
查看答案和解析>>

 的导数
的导数 处取到极大值,则
处取到极大值,则 的取值范围是 .
的取值范围是 . 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案