解答:解:【法一】(Ⅰ)当PC⊥AB时,作P在AB上的射影D,连接CD,则AB⊥平面PCD,∴AB⊥CD,∴D是AB的中点,
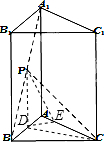
又PD∥AA
1,∴P也是A
1B的中点,即A
1P:PB=1.
反之当A
1P:PB=1时,取AB的中点D',连接CD'、PD'.
∵△ABC为正三角形,∴CD'⊥AB.
由于P为A
1B的中点时,PD'∥A
1A
∵A
1A⊥平面ABC,∴PD'⊥平面ABC,∴PC⊥AB.…6′
(Ⅱ)当A
1P:PB=2:3时,作P在AB上的射影D,则PD⊥底面ABC.
作D在AC上的射影E,连接PE,则PE⊥AC,∴∠DEP为二面角P-AC-B的平面角.
又∵PD∥AA
1,∴
==,∴
AD=a.
∴
DE=AD•sin60°=a,
又∵
=,∴
PD=a,∴
tan∠PED==,∴P-AC-B的大小为∠PED=60°.…12
【法二】以A为原点,AB为x轴,过A点与AB垂直的直线为y轴,AA
1为z轴,建立空间直角坐标系A-xyz,如图所示,
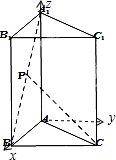
设P(x,0,z),则B(a,0,0)、A
1(0,0,a)、
C(,,0).
(Ⅰ)由
•=0得
(x-,-,z)•(a,0,0)=0,即
(x-)•a=0,
∴
x=a,即P为A
1B的中点,也即A
1P:PB=1时,PC⊥AB.…4′
(Ⅱ)当A
1P:PB=2:3时,P点的坐标是
(,0,).
取
=(3,-,-2).则
•=(3,-,-2)•(,0,)=0,
•=(3,-,-2)•(,,0)=0.
∴
是平面PAC的一个法向量.
又平面ABC的一个法向量为
=(0,0,1).
∴
cos<,>==,∴二面角P-AC-B的大小是60°.…(12分)

 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
 设P(x,0,z),则B(a,0,0)、A1(0,0,a)、C(
设P(x,0,z),则B(a,0,0)、A1(0,0,a)、C(

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案 如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点. (2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
(2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为