
 的渐近线在第一象限内的部分上一动点,F为双曲线C的右焦点,A为双曲线C的右准线与x轴的交点,e是双曲线C的离心率,则∠APF的最大值为( )
的渐近线在第一象限内的部分上一动点,F为双曲线C的右焦点,A为双曲线C的右准线与x轴的交点,e是双曲线C的离心率,则∠APF的最大值为( )
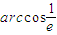


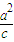 ,0),F(c,0),P(at,bt) 由直线的斜率公式,得KPF=
,0),F(c,0),P(at,bt) 由直线的斜率公式,得KPF=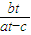 ,KPA=
,KPA=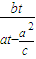 ,再利用根据到角公式,得tan∠APF的表达式,最后利用基本不等式求得tan∠APF的最大值,以及取得取大值时有:
,再利用根据到角公式,得tan∠APF的表达式,最后利用基本不等式求得tan∠APF的最大值,以及取得取大值时有: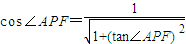 =
=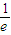 ,结合反三角函数即可表示出∠APF的最大值.
,结合反三角函数即可表示出∠APF的最大值.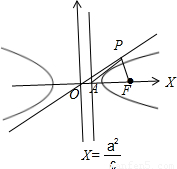 解:由题意得:A(
解:由题意得:A(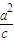 ,0),F(c,0),P(at,bt)
,0),F(c,0),P(at,bt) 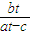 ,KPA=
,KPA=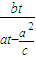
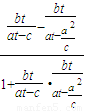
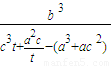
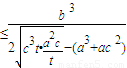 =
=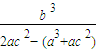 =
=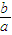
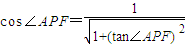 =
=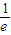
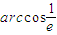


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、arcsin
| ||||
B、arccos
| ||||
C、arctan
| ||||
D、arccot
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆市南开中学高三(下)3月月考数学试卷(文科)(解析版) 题型:选择题
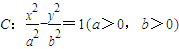 的渐近线在第一象限内的部分上一动点,F为双曲线C的右焦点,A为双曲线C的右准线与x轴的交点,e是双曲线C的离心率,则∠APF的余弦的最小值为( )
的渐近线在第一象限内的部分上一动点,F为双曲线C的右焦点,A为双曲线C的右准线与x轴的交点,e是双曲线C的离心率,则∠APF的余弦的最小值为( )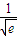
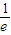
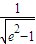
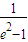
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com