练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在四棱锥中，四边形为平行四边形，三角形为等边三角形，已知，，，.

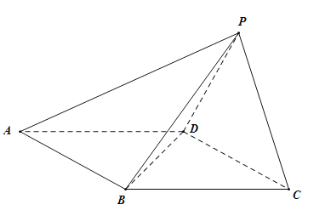
    （1）求证：

    （2）求直线与面所成的角的正弦值.

    【答案】（1）证明见解析；（2）.

    【解析】

    （1）取的中点， 根据线面垂直判定定理得平面，即得，再根据勾股定理逆定理得结果；

    （2）先建立空间直角坐标系，求平面一个法向量，再利用向量数量积求向量夹角，最后根据线面角与向量夹角关系得结果.

    （1）设的中点为，连接与，

    因为是等边三角形，所以，又因为，所以平面，则，， ，所以是等腰直角三角形，且

    （2）由（1）可知平面，即平面平面，又因为，，

    所以

    以为原点，过在所在平面内作的垂线为轴，所在直线为轴建立空间直角坐标系

    则点

    ，

    设平面的法向量， 令，则则，所以

    因此直线与面所成的角的正弦值

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝ax2+2ax﹣lnx﹣1，a∈R．

    （1）当a时，求f（x）的单调区间及极值；

    （2）若a为整数，且不等式f（x）≥x对任意x∈（0，+∞）恒成立，求a的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于函数有下述四个结论：

    ①是偶函数；②的最大值为；

    ③在有个零点；④在区间单调递增.

    其中所有正确结论的编号是（ ）

    A.①②B.①③C.②④D.①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大型公司为了切实保障员工的健康安全，贯彻好卫生防疫工作的相关要求，决定在全公司范围内举行一次乙肝普查，为此需要抽验960人的血样进行化验，由于人数较多，检疫部门制定了下列两种可供选择的方案.

    方案①：将每个人的血分别化验，这时需要验960次.

    方案②：按个人一组进行随机分组，把从每组个人抽来的血混合在一起进行检验，如果每个人的血均为阴性，则验出的结果呈阴性，这个人的血就只需检验一次；否则，若呈阳性，则需对这个人的血样再分别进行一次化验，这样，该组个人的血总共需要化验次.

    假设此次普查中每个人的血样化验呈阳性的概率为，且这些人之间的试验反应相互独立.

    （1）设方案②中，某组个人中每个人的血化验次数为，求的分布列；

    （2）设，试比较方案②中，分别取2，3，4时，各需化验的平均总次数；并指出在这三种分组情况下，相比方案①，化验次数最多可以平均减少多少次？(最后结果四舍五入保留整数).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）试比较与的大小.

    （2）若函数的两个零点分别为，，

    ①求的取值范围；

    ②证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，平面，四边形为菱形．

    （Ⅰ）证明：平面；

    （Ⅱ）若，，二面角的余弦值为，求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位在2019年重阳节组织50名退休职工（男、女各25名）旅游,退休职工可以选择到甲、乙两个景点其中一个去旅游.他们最终选择的景点的结果如下表：

    男性

    女性

    甲景点

    20

    10

    乙景点

    5

    15

    （1）据此资料分析,是否有的把握认为选择哪个景点与性别有关？

    （2）按照游览不同景点用分层抽样的方法,在女职工中选取5人,再从这5人中随机抽取2人进行采访,求这2人游览的景点不同的概率.

    附：,.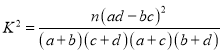

    P（）

    0.010

    0.005

    0.001

    k

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆上一点关于原点的对称点为，点， 的面积为，直线过上的点.

    （1）求的方程；

    （2）设为的短轴端点，直线过点交于，证明：四边形的两条对角线的交点在定直线上.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的偶函数f（x）在（﹣∞，0]上单调递增，且f（﹣1）＝﹣1.若f（x﹣1）+1≥0，则x的取值范围是_____；设函数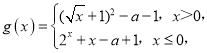若方程f（g（x））+1＝0有且只有两个不同的实数解，则实数a的取值范围为_____.

    查看答案和解析>>

    同步练习册答案