
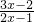 ,(x
,(x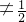 ),
), )+F(
)+F(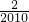 )+…+F(
)+…+F( )的值;
)的值; }是等差数列;
}是等差数列; ,求数列{anbn}的前n项和Sn.
,求数列{anbn}的前n项和Sn. =3.------------------------------(2分)
=3.------------------------------(2分) )+f(
)+f(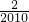 )+…+F(
)+…+F( )…(1)
)…(1) )+f(
)+f(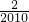 )+…+F(
)+…+F( )…(2)
)…(2) )+F(
)+F( )]=3×2009=6027,
)]=3×2009=6027,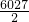 .
.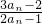 -1=
-1=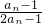 .---------(7分)
.---------(7分) =
=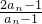 =2+
=2+
 }是以2为公差以1为首项的等差数列.----(10分)
}是以2为公差以1为首项的等差数列.----(10分)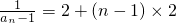 ,
, =
=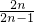 .
. ,所以anbn=
,所以anbn=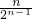 ------------------------------(12分)
------------------------------(12分)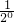 +
+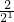 +…+
+…+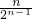 (3)
(3) Sn=
Sn=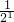 +
+ +…+
+…+ (4)
(4) Sn=
Sn=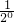 +
+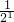 +…+
+…+ -
-
 -
-
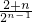 -----------------------------(14分)
-----------------------------(14分) )+f(
)+f(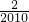 )+…+F(
)+…+F( )倒序后相加即可得到结果.
)倒序后相加即可得到结果. =
= =2+
=2+ ,所以,{
,所以,{ }是以2为公差以1为首项的等差数列.
}是以2为公差以1为首项的等差数列. ,它是一个等差数列与等比数列积的形式,利用错位相减可求数列的和.
,它是一个等差数列与等比数列积的形式,利用错位相减可求数列的和.

科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com