

(1)����Բ�ķ��̣�
(2)��ֱ��l��F��(l����ֱ������)��������Բ����A��B���㣬�߶�AB�Ĵ�ֱƽ���߽�x���ڵ�M(m,0)������m��ȡֵ��Χ.
(��)ij��������2006����д��������������㣬�ò�Ʒ����������(���ó��������)x��������������m��Ԫ(m��0)����x=3![]() (kΪ����)�����������������ò�Ʒ����������ֻ����1���.��֪2006�������ò�Ʒ�Ĺ̶�Ͷ��Ϊ8��Ԫ��ÿ����1����ò�Ʒ��Ҫ��Ͷ��16��Ԫ�����ҽ�ÿ����Ʒ�����ۼ۸�Ϊÿ����Ʒ��ƽ���ɱ���1.5��(��Ʒ�ɱ������̶�Ͷ�����Ͷ���������ʽ𣬲�������������).
(kΪ����)�����������������ò�Ʒ����������ֻ����1���.��֪2006�������ò�Ʒ�Ĺ̶�Ͷ��Ϊ8��Ԫ��ÿ����1����ò�Ʒ��Ҫ��Ͷ��16��Ԫ�����ҽ�ÿ����Ʒ�����ۼ۸�Ϊÿ����Ʒ��ƽ���ɱ���1.5��(��Ʒ�ɱ������̶�Ͷ�����Ͷ���������ʽ𣬲�������������).
(1)��2006��ò�Ʒ������y��Ԫ��ʾΪ���������m��Ԫ�ĺ�����
(2)�ó���2006��Ĵ�������Ͷ�������Ԫʱ�����ҵ��������
�⣺(1)�����⣬֪P1��P5��P2��P4�ֱ����y��Գ�.
����Բ����ΪF1����|P1F|+|P5F|=|P1F|+|P1F1|=2a.ͬ��,|P2F|+|P4F|=2a,
��|P3F|=a,
��|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5a=![]() .��a=
.��a=![]() .
.
����Բ�ķ���Ϊ![]() +y2=1.
+y2=1.
(2)�����⣬F(1��0)����l�ķ���Ϊy=k(x-1)(k��0),
������Բ����![]() +y2=1,��������(1+2k2)x2-4k2x+2k2-2=0.
+y2=1,��������(1+2k2)x2-4k2x+2k2-2=0.
��l����Բ���ҽ��㣬��l����Բ���ڲ�ͬ������A��B.
��A(x1,y1)��B(x2,y2),AB�е�Ϊ(x0,y0),
��x1+x2=![]() ,x0=
,x0=![]() (x1+x2)=
(x1+x2)=![]() ,y0=k(x0-1)=
,y0=k(x0-1)=![]() .
.
��AB�Ĵ�ֱƽ���߷���Ϊ
y-y0=![]() (x-x0).
(x-x0).
��y=0,��m=x0+ky0=![]()
![]() =
=![]() =
=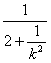 .
.
����![]() ��0,��2+
��0,��2+![]() ��2.��0��m��
��2.��0��m��![]() .
.
(��)�⣺(1)�������֪��m=0ʱ��x=1(���)����1=3-k,��k=2.
��x=![]() .
.
ÿ����Ʒ�����ۼ۸�Ϊ1.5��![]() (Ԫ),
(Ԫ),
��2006�������y=x(1.5��![]() )-(8+16x+m)
)-(8+16x+m)
=4+8x-m=4+8(![]() )-m
)-m
=-��![]() +(m+1)��+29(m��0).
+(m+1)��+29(m��0).
(2)��m��0ʱ��![]() +(m+1)��
+(m+1)��![]() =8,
=8,
��y��-8+29=21,���ҽ���![]() =m+1
=m+1![]() m=3(��Ԫ)ʱ��ymax=21(��Ԫ).
m=3(��Ԫ)ʱ��ymax=21(��Ԫ).
��ó���2006��Ĵ�������Ͷ��3��Ԫʱ,���ҵ��������,���ֵΪ21��Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����Բ�ķ���Ϊ
��ͼ����Բ�ķ���Ϊ| x2 |
| a2 |
| 2y2 |
| a2 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ��ɽ��ʡ�ij��и�����ѧ����ĩ������ѧ ���ͣ������
�� 12�֣���ͼ����Բ�ķ���Ϊ �����ҽ���ΪF������Բ�ij���ֳ�6�ȷ֣���ÿ���ȷֵ���x��Ĵ��߽���Բ�ϰ벿�ڵ�P1��P2��P3��P4��P5����㣬��|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5
�����ҽ���ΪF������Բ�ij���ֳ�6�ȷ֣���ÿ���ȷֵ���x��Ĵ��߽���Բ�ϰ벿�ڵ�P1��P2��P3��P4��P5����㣬��|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5 .
.

��1������Բ�ķ��̣�
��2����ֱ��l��F�㣨l����ֱ�����ᣩ��������Բ����A��B���㣬�߶�AB�Ĵ�ֱƽ���߽�x���ڵ�M��m,0��������m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Բ�ķ���Ϊ
��ͼ����Բ�ķ���Ϊ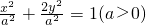 �����ҽ���ΪF������Բ�ij���ֳ�6�ȷ֣���ÿ���ȷֵ���x��Ĵ��߽���Բ�ϰ벿�ڵ�P1��P2��P3��P4��P5����㣬��|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5
�����ҽ���ΪF������Բ�ij���ֳ�6�ȷ֣���ÿ���ȷֵ���x��Ĵ��߽���Բ�ϰ벿�ڵ�P1��P2��P3��P4��P5����㣬��|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5 ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ��ɽ��ʡ�ij�����У�����������ϣ���ĩ��ѧ�Ծ��������棩 ���ͣ������
 �����ҽ���ΪF������Բ�ij���ֳ�6�ȷ֣���ÿ���ȷֵ���x��Ĵ��߽���Բ�ϰ벿�ڵ�P1��P2��P3��P4��P5����㣬��|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5
�����ҽ���ΪF������Բ�ij���ֳ�6�ȷ֣���ÿ���ȷֵ���x��Ĵ��߽���Բ�ϰ벿�ڵ�P1��P2��P3��P4��P5����㣬��|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5 ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com