
【题目】如图,已知直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),过线段
左侧),过线段![]() (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线![]() ,使得直线
,使得直线![]() 与抛物线
与抛物线![]() 在点
在点![]() 处的切线平行,设直线
处的切线平行,设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点.
两点.
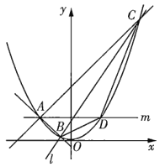
(1)记直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明:
,证明:![]() ;
;
(2)若![]() ,求
,求![]() 的面积.
的面积.
科目:高中数学 来源: 题型:
【题目】A、B两同学参加数学竞赛培训,在培训期间,他们参加了8次测验,成绩(单位:分)记录如下:
A 71 62 72 76 63 70 85 83
B 73 84 75 73 7![]() 8
8![]() 76 85
76 85
B同学的成绩不慎被墨迹污染(![]() ,
,![]() 分别用m,n表示).
分别用m,n表示).
(1)用茎叶图表示这两组数据,现从A、B两同学中选派一人去参加数学竞赛,你认为选派谁更好?请说明理由(不用计算);
(2)若B同学的平均分为78,方差![]() ,求m,n.
,求m,n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() ,其中
,其中![]() ,且
,且![]() ,若对
,若对![]() ,
,![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() ,则称数集
,则称数集![]() 具有性质
具有性质![]() .
.
(1)分别判断数集![]() 与数集
与数集![]() 是否具有性质
是否具有性质![]() ,说明理由;
,说明理由;
(2)已知数集![]() 具有性质
具有性质![]() ,判断数列
,判断数列![]() ,
,![]() ,…,
,…,![]() 是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的准线经过点
的准线经过点![]() ,过
,过![]() 的焦点
的焦点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,则下列结论正确的是( )
两点,则下列结论正确的是( )
A.![]() B.
B.![]() 的最小值为16
的最小值为16
C.四边形![]() 的面积的最小值为64D.若直线
的面积的最小值为64D.若直线![]() 的斜率为2,则
的斜率为2,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点F2是双曲线![]() 的右焦点,动点A在双曲线左支上,直线l1:tx﹣y+t﹣2=0与直线l2:x+ty+2t﹣1=0的交点为B,则|AB|+|AF2|的最小值为( )
的右焦点,动点A在双曲线左支上,直线l1:tx﹣y+t﹣2=0与直线l2:x+ty+2t﹣1=0的交点为B,则|AB|+|AF2|的最小值为( )
A.8B.![]() C.9D.
C.9D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的英明领导下,在全国人民的坚定支持下,中国的抗击“新型冠状肺炎”战役取得了阶段性胜利,现在摆在我们大家面前的是有序且安全的复工复产.某商场为了提振顾客的消费信心,对某中型商品实行分期付款方式销售,根据以往资料统计,顾客购买该商品选择分期付款的期数ξ的分布列为

其中0<a<1,0<b<1.
(1)求购买该商品的3位顾客中,恰有1位选择分4期付款的概率;
(2)商场销售一件该商品,若顾客选择分4期付款,则商场获得的利润为2000元;若顾客选择分5期付款,则商场获得的利润为2500元;若顾客选择分6期付款,则商场获得的利润为3000元,假设该商场销售两件该商品所获得的利润为X(单位:元),
(i)设X=5500时的概率为m,求当m取最大值时,利润X的分布列和数学期望;
(ii)设某数列{xn}满足x1=0.4,xn=a,2xn+1=b,若a<0.25,求n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
=1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
(1) 求椭圆C的方程;
(2) 设椭圆的左顶点为A,记直线AP,AQ的斜率分别为k1,k2.①若m=0,求k1k2的值;②若k1k2=-![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,
,![]()
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,是否存在q的某些取值,使数列
,是否存在q的某些取值,使数列![]() 中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由.
中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由.
(3)若![]() ,是否存在
,是否存在![]() ,使数列
,使数列![]() 中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由.
中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com