
| A. | y=sin$\frac{x}{2}$ | B. | y=sin x | C. | y=-tan x | D. | y=-cos 2x |
分析 根据三角函数的图象及性质,依次判断各选项即可.
解答 解:对于A:y=sin$\frac{x}{2}$,其周期T=$\frac{2π}{\frac{1}{2}}=4π$,∴A不对.
对于B:y=sin x,其周期T=$\frac{2π}{1}=2π$,∴B不对.
对于C:y=-tan x,其周期T=$\frac{π}{1}=π$,在区间(0,$\frac{π}{2}$)上为减函数,∴C不对.
对于D:y=-cos 2x,其周期T=$\frac{2π}{2}=π$,cos 2x在区间(0,$\frac{π}{2}$)上为减函数,则y=y=-cos 2x,在区间(0,$\frac{π}{2}$)上为增函数,故选D.
点评 本题主要考查三角函数的图象和性质,比较基础.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | (-∞,2] | C. | (0,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持希拉里 | 支持特朗普 | 合计 | |
| 男员工 | |||
| 女员工 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的一条对称轴为x=$\frac{5π}{12}$ | |
| B. | 存在φ使得f(x)在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递减 | |
| C. | f(x)的一个对称中心为($\frac{5π}{12}$,0) | |
| D. | 存在φ使得f(x)在区间[$\frac{π}{12}$,$\frac{7π}{12}$]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
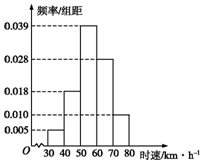 某时段内共有100辆汽车经过某一雷达地区,汽车时速的频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )
某时段内共有100辆汽车经过某一雷达地区,汽车时速的频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )| A. | 38 | B. | 28 | C. | 10 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
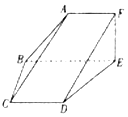 如图,平面ABEF⊥平面CBED,四边形ABEF为直角梯形,∠AFE=∠FEB=90°,四边形CBED为等腰梯形,CD∥BE,且BE=2AF=2CD=2BC=2EF=4.
如图,平面ABEF⊥平面CBED,四边形ABEF为直角梯形,∠AFE=∠FEB=90°,四边形CBED为等腰梯形,CD∥BE,且BE=2AF=2CD=2BC=2EF=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com