
【题目】已知函数![]() .
.
(1)当![]() 时,求满足
时,求满足![]() 的
的![]() 的取值;
的取值;
(2)若函数![]() 是定义在
是定义在![]() 上的奇函数
上的奇函数
①存在![]() ,不等式
,不等式![]() 有解,求
有解,求![]() 的取值范围;
的取值范围;
②若函数![]() 满足
满足![]() ,若对任意
,若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() (2) ①
(2) ①![]() ,②6
,②6
【解析】试题分析:(1)根据![]() ,可将方程
,可将方程![]() 转化为一元二次方程:
转化为一元二次方程: ![]() ,再根据指数函数范围可得
,再根据指数函数范围可得![]() ,解得
,解得![]() (2) ①先根据函数奇偶性确定
(2) ①先根据函数奇偶性确定![]() 值:
值: ![]() ,再利用单调性定义确定其单调性:在R上递减.最后根据单调性转化不等式
,再利用单调性定义确定其单调性:在R上递减.最后根据单调性转化不等式![]() 为
为![]() 即
即![]() 在
在![]() 时有解,根据判别式大于零可得
时有解,根据判别式大于零可得![]() 的取值范围②先求函数
的取值范围②先求函数![]() :
: ![]() ,则
,则![]() ,因此不等式可转化为一元二次不等式,并将其变量分离得:
,因此不等式可转化为一元二次不等式,并将其变量分离得: ![]() 的最小值,其中
的最小值,其中![]() ,利用基本不等式求最值得
,利用基本不等式求最值得![]()
试题解析:(1) 由题意, ![]() ,化简得
,化简得![]()
解得![]() ,
,
所以![]()
(2) 因为![]() 是奇函数,所以
是奇函数,所以![]() ,所以
,所以![]()
化简并变形得: ![]()
要使上式对任意的![]() 成立,则
成立,则![]()
解得: ![]() ,因为
,因为![]() 的定义域是
的定义域是![]() ,所以
,所以![]() 舍去
舍去
所以![]() , 所以
, 所以![]()
①![]()
对任意![]() 有:
有:
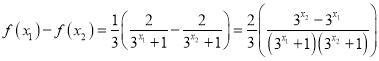
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因此![]() 在R上递减.
在R上递减.
因为![]() ,所以
,所以![]() ,
,
即![]() 在
在![]() 时有解
时有解
所以![]() ,解得:
,解得: ![]() ,
,
所以![]() 的取值范围为
的取值范围为![]()
②因为![]() ,所以
,所以![]()
即![]()
所以![]()
不等式![]() 恒成立,
恒成立,
即![]() ,
,
即: ![]() 恒成立
恒成立
令![]() ,则
,则![]() 在
在![]() 时恒成立
时恒成立
令![]() ,
, ![]() ,
,
![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减
上单调递减
![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增
上单调递增
所以![]() ,所以
,所以![]()
所以,实数m的最大值为6


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】在互联网时代,网校培训已经成为青年学习的一种趋势,假设某网校的套题每日的销售量![]() (单位:千套)与销售价格
(单位:千套)与销售价格![]() (单位:元/套)满足的关系式
(单位:元/套)满足的关系式![]() (
(![]() ,
,![]() 为常数),其中
为常数),其中![]() 与
与![]() 成反比,
成反比,![]() 与
与![]() 的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.
的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.
(1) 求![]() 的表达式;
的表达式;
(2) 假设网校的员工工资,办公等所有开销折合为每套题3元(只考虑销售出的套数),试确定销售价格![]() 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆x2+y2-6x-8y+21=0和直线kx-y-4k+3=0.
(1)若直线和圆总有两个不同的公共点,求k的取值集合
(2)求当k取何值时,直线被圆截得的弦最短,并求这最短弦的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次“知识竞赛”活动中,有![]() 四道题,其中
四道题,其中![]() 为难度相同的容易题,
为难度相同的容易题, ![]() 为中档题,
为中档题, ![]() 为较难题,现甲、乙两位同学均需从四道题目中随机抽取一题作答.
为较难题,现甲、乙两位同学均需从四道题目中随机抽取一题作答.
(1)求甲、乙两位同学所选的题目难度相同的概率;
(2)求甲所选题目的难度大于乙所选题目的难度的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com