
【题目】如图所示,茎叶图记录了甲、乙两组各4名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中以X表示。

(1)如果x=8,求乙组同学植树棵数的平均数和方差;
(2)如果x=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列。
【答案】(1)平均数![]() ,方差
,方差![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)当x=8时,利用茎叶图能求出乙组同学植树棵数的平均数和方差.
(2)当x=9时,由茎叶图可知,甲组同学的植树棵树是:9,9,11,11;乙组同学的植树棵数是:9,8,9,10.这两名同学植树总棵数Y的可能取值为17,18,19,20,21,分别求出相应的概率,由此能求出这两名同学的植树总棵数Y的分布列.
(1)当x=8时,由茎叶图可知,乙组同学的植树棵数是8,8,9,10,
所以平均数为![]() ;
;
方差为![]() 。
。
(2)当x=9时,由茎叶图可知,甲组同学的植树棵数是9,9,11,11;乙组同学的植树棵数是9,8,9,10。
分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能的结果,这两名同学植树总棵数Y的可能取值为17,18,19,20,21。
事件“Y=17”等价于“甲组选出的同学植树9棵,乙组选出的同学植树8棵”,
所以该事件有2种可能的结果,因此P(Y=17)=![]() =
=![]() 。
。
同理可得P(Y=18)=![]() ;P(Y=19)=
;P(Y=19)=![]() ;
;
P(Y=20)=![]() ;P(Y=21)=
;P(Y=21)=![]() 。
。
所以随机变量Y的分布列为
Y | 17 | 18 | 19 | 20 | 21 |
P |
|
|
|
|
|


科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=![]() .
.
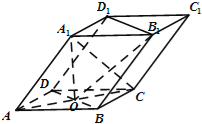
(Ⅰ)证明:平面A1BD∥平面CD1B1;
(Ⅱ)求三棱柱ABD﹣A1B1D1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙二人用4张扑克牌![]() 分别是红桃2,红桃3,红桃4,方片4玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
分别是红桃2,红桃3,红桃4,方片4玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
![]() 写出甲、乙二人抽到的牌的所有情况;
写出甲、乙二人抽到的牌的所有情况;
![]() 甲乙约定,若甲抽到的牌的牌面数字比乙大,则甲胜;否则乙胜,你认为此约定是否公平?请说明理由.
甲乙约定,若甲抽到的牌的牌面数字比乙大,则甲胜;否则乙胜,你认为此约定是否公平?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的图象为C,则下列结论中正确的是( )
的图象为C,则下列结论中正确的是( )
A.图象C关于直线![]() 对称
对称
B.图象C关于点![]() 对称
对称
C.函数![]() 在区间
在区间![]() 内是增函数
内是增函数
D.把函数![]() 的图象上点的横坐标缩短为原来的一半(纵坐标不变)可以得到图象C
的图象上点的横坐标缩短为原来的一半(纵坐标不变)可以得到图象C
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)写出下列两组诱导公式:
①关于![]() 与
与![]() 的诱导公式;
的诱导公式;
②关于![]() 与
与![]() 的诱导公式.
的诱导公式.
(2)从上述①②两组诱导公式中任选一组,用任意角的三角函数定义给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,关于
,关于![]() 的方程
的方程![]() ,给出下列四个命题,其中假命题的个数是( )
,给出下列四个命题,其中假命题的个数是( )
①存在实数![]() ,使得方程恰有
,使得方程恰有![]() 个不同的实根;
个不同的实根;
②存在实数![]() ,使得方程恰有
,使得方程恰有![]() 个不同的实根;
个不同的实根;
③存在实数![]() ,使得方程恰有
,使得方程恰有![]() 个不同的实根;
个不同的实根;
④存在实数![]() ,使得方程恰有
,使得方程恰有![]() 个不同的实根.
个不同的实根.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象如图所示
的一段图象如图所示

(1)求![]() 的解析式;
的解析式;
(2)求![]() 的单调增区间,并指出
的单调增区间,并指出![]() 的最大值及取到最大值时
的最大值及取到最大值时![]() 的集合;
的集合;
(3)把![]() 的图象向左至少平移多少个单位,才能使得到的图象对应的函数为偶函数.
的图象向左至少平移多少个单位,才能使得到的图象对应的函数为偶函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com