
在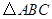 中,内角
中,内角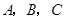 对边的边长分别是
对边的边长分别是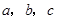 ,已知
,已知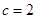 ,
, .
.
(Ⅰ)若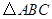 的面积等于
的面积等于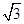 ,求
,求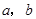 ;
;
(Ⅱ)若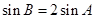 ,求
,求 的面积.
的面积.
科目:高中数学 来源: 题型:解答题
位于A处的雷达观测站,发现其北偏东45°,与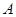 相距20
相距20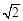 海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东
海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东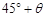
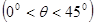 的C处,
的C处,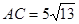 .在离观测站A的正南方某处E,
.在离观测站A的正南方某处E,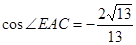
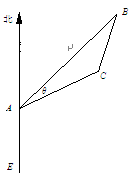
(1)求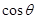 ; (2)求该船的行驶速度v(海里/小时);
; (2)求该船的行驶速度v(海里/小时);
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)如图,甲船以每小时30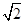 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10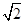 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?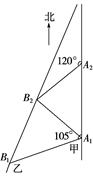
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
欲测河的宽度,在一岸边选定B、C两点,望对岸的标记物A,测得∠CBA=45°,∠BCA=75°,BC=120 m,求河宽.(精确到0.01 m)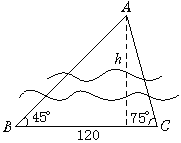
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分,第1小题6分,第2小题8分)
已知函数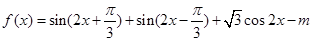 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1.
(1) 求m的值,并求f(x)的单调递增区间;
(2) 在△ABC中,角A、B、C的对边a、b、c,若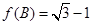 ,且
,且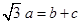 ,试判断△ABC的形状.
,试判断△ABC的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com