
对于给定首项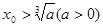 ,由递推公式
,由递推公式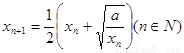 得到数列
得到数列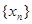 ,对于任意的
,对于任意的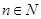 ,都有
,都有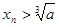 ,用数列
,用数列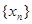 可以计算
可以计算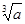 的近似值。
的近似值。
(1)取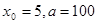 ,计算
,计算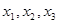 的值(精确到0.01);归纳出
的值(精确到0.01);归纳出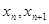 的大小关系;
的大小关系;
(2)当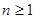 时,证明:
时,证明: ;
;
(3)当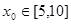 时,用数列
时,用数列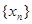 计算
计算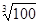 的近似值,要求
的近似值,要求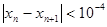 ,请你估计n,并说明理由
,请你估计n,并说明理由
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 3 | a |
| 1 |
| 2 |
|
| 3 | a |
| 3 | a |
| 1 |
| 2 |
| 3 | 100 |
查看答案和解析>>
科目:高中数学 来源:2011届上海市普通高等学校高三春季招生数学卷doc 题型:解答题
对于给定首项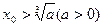 ,由递推公式
,由递推公式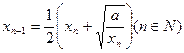 得到数列
得到数列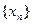 ,对于任意的
,对于任意的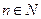 ,都有
,都有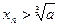 ,用数列
,用数列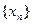 可以计算
可以计算 的近似值。
的近似值。
(1)取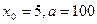 ,计算
,计算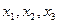 的值(精确到0.01);归纳出
的值(精确到0.01);归纳出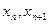 的大小关系;
的大小关系;
(2)当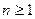 时,证明:
时,证明: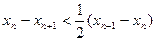 ;
;
(3)当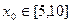 时,用数列
时,用数列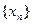 计算
计算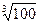 的近似值,要求
的近似值,要求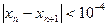 ,请你估计n,并说明理由
,请你估计n,并说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
对于给定首项![]() ,由递推式
,由递推式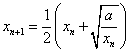
![]() 得到数列
得到数列![]() ,且对于任意的
,且对于任意的![]() ,都有
,都有![]() ,用数列
,用数列![]() 可以计算
可以计算![]() 的近似值.
的近似值.
(1) 取![]() ,
,![]() ,计算
,计算![]() 的值(精确到
的值(精确到![]() ),归纳出
),归纳出![]() ,
,![]() 的大小关系;
的大小关系;
(2) 当![]() 时,证明
时,证明![]() ;
;
(3) 当![]() 时,用数列
时,用数列![]() 计算
计算![]() 的近似值,要求
的近似值,要求![]() ,请你估计
,请你估计![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年上海市春季高考数学试卷(解析版) 题型:解答题
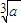 (a>0),由递推公式xn+1=
(a>0),由递推公式xn+1= (xn+
(xn+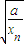 )(n∈N)得到数列{xn},对于任意的n∈N,都有xn>
)(n∈N)得到数列{xn},对于任意的n∈N,都有xn>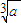 ,用数列{xn}可以计算
,用数列{xn}可以计算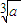 的近似值.
的近似值. (xn-1-xn);
(xn-1-xn);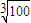 的近似值,要求|xn-xn+1|<10-4,请你估计n,并说明理由.
的近似值,要求|xn-xn+1|<10-4,请你估计n,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com