
| A. | [1,$\frac{5}{3}$] | B. | [0,1] | C. | [1,$\frac{8}{3}$] | D. | [0,$\frac{5}{3}$] |
分析 根据已知的约束条件,画出可行域,分别求出各角点的坐标,分析目标z=$\frac{x+y+2}{x+1}$函数的几何意义,将最优解代入得到目标函数的最值,进而可得取值范围.
解答 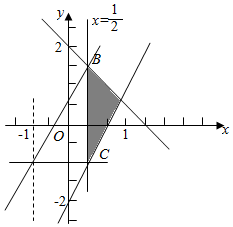 解:不等式组表示的平面区域如下图所示:
解:不等式组表示的平面区域如下图所示:
∵动点P(x,y)在可行域运动,
z=$\frac{x+y+2}{x+1}$=1+$\frac{y+1}{x+1}$,
表示(x,y)点与(-1,-1)点连线的斜率再加1,
故当P与C重合时,z取最小值1+0=1,
当P与B重合时,z取最大值1+$\frac{5}{3}$=$\frac{8}{3}$,
故z的取值范围是[1,$\frac{8}{3}$],
故选:B.
点评 本题考查的知识点是简单线性规划的应用,其中角点法是解答此类问题最常用的办法,一定要熟练掌握.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
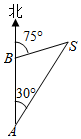 如图,一艘船下午13:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,14:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距9$\sqrt{2}$海里,则此船的航速为36海里/小时.
如图,一艘船下午13:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,14:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距9$\sqrt{2}$海里,则此船的航速为36海里/小时.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
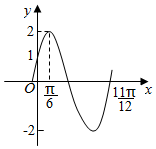 已知函数f(x)=Asin(ωx+φ),|φ|<$\frac{π}{2}$,图象如下,请回答下列问题.
已知函数f(x)=Asin(ωx+φ),|φ|<$\frac{π}{2}$,图象如下,请回答下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1) | B. | (-5,1) | ||
| C. | (-5,-1) | D. | (-5,-1)∪(-1,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:选择题
“ ”是“不等式
”是“不等式 ”的( )
”的( )
A.充分不必要条件 B.充分必要条件
C.必要不充分条件 D.非充分必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com