
【题目】如图 ,在棱长为 a 的正方体ABCD-A1 B1C1 D1 中,E 、F 分别 是棱 AB 与BC 的中点.
(1)求二 面角 B-FB1-E 的大小;
(2)求点 D 到平面B1EF 的距离;
(3)在棱 DD1 上能否找到一点 M, 使 BM ⊥平面EFB1 ? 若能, 试确定点 M 的位置;若不能, 请说明理由.

【答案】(1) ![]() (2) a. (3) M为DD1的中心
(2) a. (3) M为DD1的中心
【解析】
(1)如图 ,作BH ⊥B1 F ,垂足为H , 连结 EH .
由正方体性质知EB ⊥面BB1 F,则 BH是EH 在面BB1 F内的射影.
由三垂线定理可知,EH⊥B1 F .
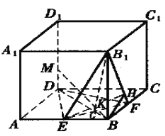
从而,∠EHB是二面角E-B1 F-B 的平面角.
在Rt△EBH中,由![]() ,知
,知![]() .
.
故![]() ,即二面角B-B1F-E的大小为
,即二面角B-B1F-E的大小为![]() .
.
(2)因![]() 为公共边,
为公共边,
故![]() .
.
设点 D 到面B1EF 的距离为h .
由![]() ,得
,得![]() .
.
故![]() ,即点 D 到面B1EF 的距离为a.
,即点 D 到面B1EF 的距离为a.
(3)设 EF与BD 交于G , 连 B1G.
因 为 EF ⊥ BD , EF ⊥ BB1 , 所 以 EF ⊥面 BB1D1D , 面 B1 EF ⊥面 BB1D1D .
在面 BB1 D1D 内作 BK ⊥B1G 于 K , 延长后交DD1于 M.
由两平面垂直的性质定理知 BM ⊥面 B1EF , 即在 DD1上存在适合条件的点 M .
在平面 BB1D1D 中, 因△B1BG ∽△BDM , 故![]() .
.
又![]() ,故
,故![]() ,M为DD1的中心.
,M为DD1的中心.


科目:高中数学 来源: 题型:
【题目】为了传承经典,促进学生课外阅读,某校从高中年级和初中年级各随机抽取100名学生进行有关对中国四大名著常识了解的竞赛,图1和图2分别是高中年级和初中年级参加竞赛的学生成绩按照![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
(1)完成下列![]() 的列联表,并回答是否有
的列联表,并回答是否有![]() 的把握认为“两个学段的学生对四大名著的了解有差异”?
的把握认为“两个学段的学生对四大名著的了解有差异”?
成绩小于60分的人数 | 成绩不小于60的人数 | 合计 | |
初中年级 | |||
高中年级 | |||
合计 |
(2)规定竞赛成绩不少于70分的为优秀,按分层抽样的方法从高中,初中年级优秀学生中抽取5人进行复赛,在复赛人员中选3人进行面试,记面试人员中来自初中段的为随机变量X,求随机变量X的分布列与期望.
![]() 其中
其中![]()
附表:
| 0.10 | 0.05 | span>0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】同学们刚刚结束了史上最长寒假,经高二各班数学老师了解,同学们每天沉迷于学习中不能自拔,每天认真完成作业,作业正确率很高,为同学们点赞!某个周日一位同学正在三河滩锻炼身体,突然接到级部通知回家开网络学生会,从三河滩某处A到对岸公路BC的距离AB为2km, B处与家C间的距离为4km,从A到C,必须先步行到BC上的某一点D,步行速度为5km/h,再乘电动车到C,电动车车速为10km/h,记![]()
(1)试将由A到C所用的时间t表示为![]() 的函数
的函数![]() ;
;
(2)间![]() 为多少时,由A到C所用的时间t最少?
为多少时,由A到C所用的时间t最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线![]() (a为正常数)与
(a为正常数)与![]() 在x轴上方仅有一个公共点P.
在x轴上方仅有一个公共点P.
(1)求实数m的取值范围(用a表示);
(2)O为原点,若![]() 与x轴的负半轴交于点A,当
与x轴的负半轴交于点A,当![]() 时,试求△OAP的面积的最大值(用a表示).
时,试求△OAP的面积的最大值(用a表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() 是抛物线
是抛物线![]() 上的任意一点.当
上的任意一点.当![]() 轴时,
轴时,![]() 的面积为4(
的面积为4(![]() 为坐标原点).
为坐标原点).
(1)求抛物线![]() 的方程;
的方程;
(2)若![]() ,连接
,连接![]() 并延长交抛物线
并延长交抛物线![]() 于
于![]() ,点
,点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,且
轴的交点,且![]() 为直角三角形,求点
为直角三角形,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古装电视剧《知否》中,甲乙两人进行一种投壶比赛,比赛投中得分情况分“有初”“贯耳”“散射”“双耳”“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为![]() ,投中“贯耳”的概率为
,投中“贯耳”的概率为![]() ,投中“散射”的概率为
,投中“散射”的概率为![]() ,投中“双耳”的概率为
,投中“双耳”的概率为![]() ,投中“依竿”的概率为
,投中“依竿”的概率为![]() ,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎/肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID—19),简称“新冠肺炎”.下图是2020年1月15日至1月24日累计确诊人数随时间变化的散点图.
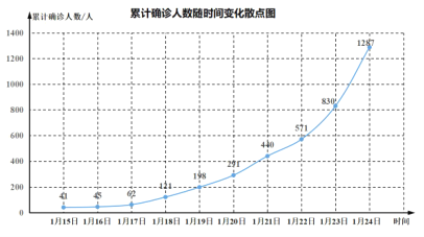
为了预测在未釆取强力措施下,后期的累计确诊人数,建立了累计确诊人数y与时间变量t的两个回归模型,根据1月15日至1月24日的数据(时间变量t的值依次1,2,…,10)建立模型![]() 和
和![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
(2根据(1)的判断结果及附表中数据,建立y关于x的回归方程;
(3)以下是1月25日至1月29日累计确诊人数的真实数据,根据(2)的结果回答下列问题:
时间 | 1月25日 | 1月26日 | 1月27日 | 1月28日 | 1月29日 |
累计确诊人数的真实数据 | 1975 | 2744 | 4515 | 5974 | 7111 |
(ⅰ)当1月25日至1月27日这3天的误差(模型预测数据与真实数据差值的绝对值与真实数据的比值)都小于0.1则认为模型可靠,请判断(2)的回归方程是否可靠?
(ⅱ)2020年1月24日在人民政府的强力领导下,全国人民共同采取了强力的预防“新冠肺炎”的措施,若采取措施5天后,真实数据明显低于预测数据,则认为防护措施有效,请判断预防措施是否有效?
附:对于一组数据(![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为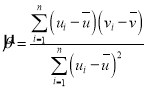 ,
,![]() .
.
参考数据:其中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
5.5 | 390 | 19 | 385 | 7640 | 31525 | 154700 | 100 | 150 | 225 | 338 | 507 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究公司为了调查公众对某事件的关注程度,在某年的连续6个月内,月份![]() 和关注人数
和关注人数![]() (单位:百)(
(单位:百)(![]() )数据做了初步处理,得到下面的散点图及一些统计量的值.
)数据做了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
17.5 | 35 | 36.5 |
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明,并建立y关于x的回归方程;
(2)经统计,调查材料费用v(单位:百元)与调查人数满足函数关系![]() ,求材料费用的最小值,并预测此时的调查人数;
,求材料费用的最小值,并预测此时的调查人数;
(3)现从这6个月中,随机抽取3个月份,求关注人数不低于1600人的月份个数![]() 分布列与数学期望.
分布列与数学期望.
参考公式:相关系数 ,若
,若![]() ,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)若数列![]() 是等差数列,且
是等差数列,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)若数列![]() 满足
满足![]() (
(![]() ),且
),且![]() ,求证:
,求证:![]() 是等差数列;
是等差数列;
(3)设数列![]() 是等比数列,试探究当正实数
是等比数列,试探究当正实数![]() 满足什么条件时,数列
满足什么条件时,数列![]() 具有如下性质
具有如下性质![]() :对于任意的
:对于任意的![]() (
(![]() ),都存在
),都存在![]() ,使得
,使得![]() ,写出你的探究过程,并求出满足条件的正实数
,写出你的探究过程,并求出满足条件的正实数![]() 的集合.
的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com