分析:(1)利用向量共线定理即可得出;
(2)令sinx=t∈[-1,1],通过分类讨论利用二次函数的单调性即可得出;
(3)通过分类讨论,利用一元一次不等式、一元二次不等式的解法即可得出.
解答:解:(1)∵
=(y-m,sinx),
=(sinx-2m,1),且
∥
∴y-m=sinx(sinx-2m),∴y=f(x)=sinx
2-2msinx+m,x∈R
(2)令sinx=t,则y=f(x)=t
2-2mt+m=h(t)=(t-m)
2+m-m
2,t∈[-1,1].
①当m>1时,t=1时h(t)取得最小值,h(1)=1-m;
②当-1≤m≤1时,t=m时h(t)取得最小值,h(m)=-m
2+m;
③当m<-1时,t=-1时h(t)取得最小值,h(-1)=1+3m.
∴g(m)=
| | 1-m,m>1 | | -m2+m,-1≤m≤1 | | 1+3m,m<-1 |
| |
.
(3)∵g(m)>-2.
∴①当m>1时,1-m>-2,解得1<m<3;
②当-1≤m≤1时,-m
2+m>-2,解得-1<m≤1;
③当m<-1时,1+3m>-2,解得m∈∅.
综上可知:g(m)>-2的解集为(-1,3).
点评:熟练掌握向量共线定理、换元法、分类讨论、二次函数的单调性、一元一次不等式、一元二次不等式的解法等是解题的关键.



 阅读快车系列答案
阅读快车系列答案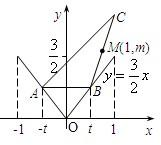 如图,函数y=
如图,函数y= (2009•湖北模拟)已知A(-1,0)、B(3,0),M、N是圆O:x2+y2=1上的两个动点,且M、N关于x轴对称,直线AM与BN交于P点.
(2009•湖北模拟)已知A(-1,0)、B(3,0),M、N是圆O:x2+y2=1上的两个动点,且M、N关于x轴对称,直线AM与BN交于P点.