
分析 (1)解绝对值不等式|f(x)|<c,结合不等式|f(x)|<c的解集为{x|-1<x<2}.我们可以构造关于b,c的方程组,解方程组即可得到b的值;
(2)由于不等式中含有参数m,故我们要对参数m进行分类讨论,分m=-$\frac{1}{2}$,m>-$\frac{1}{2}$,m<-$\frac{1}{2}$三种情况进行讨论,最后综合讨论结果即可得到答案
解答 解:(1)∵f(x)=-4x+b
∴|f(x)|<c的解集为{x|$\frac{1}{4}$(b-c)<x<$\frac{1}{4}$(b+c)}
又∵不等式|f(x)|<c的解集为{x|-1<x<2}.
∴$\frac{1}{4}$(b-c)=-1,$\frac{1}{4}$(b+c)=2
解得:b=2;
(2)由(1)得f(x)=-4x+2,
∵(x+m)•f(x)>0,化为(x+m)(x-$\frac{1}{2}$)<0,
当m=-$\frac{1}{2}$时,不等式的解集为空集,
当m>-$\frac{1}{2}$时,解集为(-m,$\frac{1}{2}$),
当m<-$\frac{1}{2}$时,解集为($\frac{1}{2}$,-m)
点评 本题考查的知识点是绝对值不等式的解法,一元二次不等式的应用,其中(1)的关键是解绝对值不等式并根据已知构造关于b,c的方程组,(2)的关键是对参数m分m=-$\frac{1}{2}$,m>-$\frac{1}{2}$,m<-$\frac{1}{2}$三种情况进行讨论.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
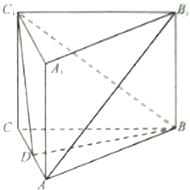 如图,在正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1中,D为AC的中点,
如图,在正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1中,D为AC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
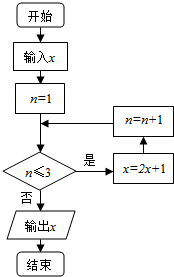 已知实数x∈[1,9],执行如图所示的程序框图,则输出的x不小于55的概率为( )
已知实数x∈[1,9],执行如图所示的程序框图,则输出的x不小于55的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com