【题目】已知数列
的前
项和为
，且
，
(1)证明：
是等比数列；
(2)求数列
的通项公式，并求出n为何值时，取得最小值，并说明理由。
（
）
【答案】(1)见解析(2)
n=15
【解析】
（1）当n=1时，a1=S1=1﹣5a1﹣85，求出a1﹣1=﹣15，当n≥2时，an=Sn﹣Sn﹣1，从而6an=5an﹣1+1，由此能证明{an﹣1}是首项为﹣15，公比为
的等比数列；
（2）由an﹣1=﹣15（）n﹣1，得Sn=n+75（）n﹣1﹣90．由此能求出n=15时，Sn取得最小值．
（1）当n=1时，a1=-14；当n≥2时，an=Sn-Sn-1=-5an+5an-1+1，所以
，
又a1-1=-15≠0，所以数列{an-1}是等比数列；
(2) 由(1)知：
，得
，
从而；
解不等式Sn<Sn+1，得
，
，当n≥15时，数列{Sn}单调递增；
同理可得，当n≤15时，数列{Sn}单调递减；故当n=15时，Sn取得最小值.
智趣寒假作业云南科技出版社系列答案科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，已知直线l：x-y-2=0，抛物线C：y2=2px(p＞0).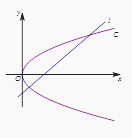
（1）若直线l过抛物线C的焦点，求抛物线C的方程；
（2）已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证：线段PQ的中点坐标为（2-p ， -p）；
②求p的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f（x）=xlnx﹣ax2+（2a﹣1）x，a∈R．
（1）令g（x）=f′（x），求g（x）的单调区间；
（2）已知f（x）在x=1处取得极大值，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，内角A，B，C所对的边分别为a，b，c，已知b+c=2acosB．
（1）证明：A=2B；
（2）若cosB= 
，求cosC的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知m、n是不同的直线，α、β是不重合的平面，则下列命题正确的是
A. 若α∥β，m
α，nβ，则m∥n
B. 若mα，nα，m∥β，n∥β，则α∥β
C. 若aα，bβ，a∥b，则α∥β
D. m、n是两异面直线，若m∥α，m∥β，且n∥α，n∥β，则α∥β
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图,M是矩形ABCD的边CD上的一点,AC与BM交于点N,BN=
BM.
(1)求证:M是CD的中点;
(2)若AB=2,BC=1,H是BM上异于点B的一动点,求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2e2x+m|x|ex+1（m∈R）有四个零点，则m的取值范围为（ ）
A.（﹣∞，﹣e﹣ 
）
B.（﹣∞，e+ ）
C.（﹣e﹣ ，﹣2）
D.（﹣∞，﹣ ）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=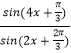 
的图象与g（x）的图象关于直线x= 
对称，则g（x）的图象的一个对称中心为（ ）
A.（ 
，0）
B.（ 
，0）
C.（ 
，0）
D.（ 
，0）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2+|x|﹣|x﹣5|+2．
（1）求不等式f（x）＜0的解集；
（2）若关于x的不等式|f（x）|≤m的整数解仅有11个，求m的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com