
【题目】已知f(x)=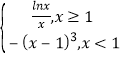 ,若关于
,若关于![]() 的方程
的方程![]() 恰好有 4 个不相等的实数解,则实数
恰好有 4 个不相等的实数解,则实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B. (
B. (![]() ) C.
) C. ![]() D. (0,
D. (0,![]() )
)
 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】若采用随机模拟的方法估计某运动员射击击中目标的概率.先由计算器给出0到9之间取整数的随机数,指定0,1,2,3表示没有击中目标,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组如下的随机数:
7327 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该运动员射击4次至少击中3次的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题,其中正确命题有( )
A.空间任意三个不共面的向量都可以作为一个基底
B.已知向量![]() ,则
,则![]() 与任何向量都不能构成空间的一个基底
与任何向量都不能构成空间的一个基底
C.![]() 是空间四点,若
是空间四点,若![]() 不能构成空间的一个基底,那么
不能构成空间的一个基底,那么![]() 共面
共面
D.已知向量![]() 组是空间的一个基底,若
组是空间的一个基底,若![]() ,则
,则![]() 也是空间的一个基底
也是空间的一个基底
查看答案和解析>>
科目:高中数学 来源: 题型:
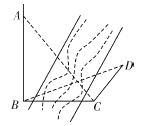
【题目】如图,为测得河对岸塔![]() 的高,先在河岸上选一点
的高,先在河岸上选一点![]() ,使
,使![]() 在塔底
在塔底![]() 的正东方向上,测得点
的正东方向上,测得点![]() 的仰角为60°,再由点
的仰角为60°,再由点![]() 沿北偏东15°方向走
沿北偏东15°方向走![]() 到位置
到位置![]() ,测得
,测得![]() ,则塔
,则塔![]() 的高是(单位:
的高是(单位:![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 10
D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
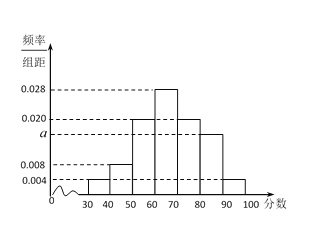
【题目】改革开放40年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各50人,进行问卷测评,所得分数的频率分布直方图如图所示.规定得分在80分以上为交通安全意识强.
安全意识强 | 安全意识不强 | 合计 | |
男性 | |||
女性 | |||
合计 |
(Ⅰ)求![]() 的值,并估计该城市驾驶员交通安全意识强的概率;
的值,并估计该城市驾驶员交通安全意识强的概率;
(Ⅱ)已知交通安全意识强的样本中男女比例为4:1,完成2×2列联表,并判断有多大把握认为交通安全意识与性别有关;
(Ⅲ)在(Ⅱ)的条件下,从交通安全意识强的驾驶员中随机抽取2人,求抽到的女性人数![]() 的分布列及期望.
的分布列及期望.
附: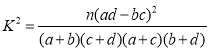 ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面ABCD平面PAD,
中,平面ABCD平面PAD,![]() ,
,![]() ,
,![]() ,
,![]() ,E是PD的中点.
,E是PD的中点.

![]() 证明:
证明:![]() ;
;
![]() 设
设![]() ,点M在线段PC上且异面直线BM与CE所成角的余弦值为
,点M在线段PC上且异面直线BM与CE所成角的余弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在第二届乌镇互联网大会中, 为了提高安保的级别同时又为了方便接待,现将其中的五个参会国的人员安排酒店住宿,这五个参会国要在![]() 、
、![]() 、
、![]() 三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有
三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有
A.![]() 种B.
种B.![]() 种
种
C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com