
【题目】已知直线l:y=kx+1(k≠0)与椭圆3x2+y2=a相交于A、B两个不同的点,记l与y轴的交点为C.
(Ⅰ)若k=1,且|AB|= ![]() ,求实数a的值;
,求实数a的值;
(Ⅱ)若 ![]() =2
=2 ![]() ,求△AOB面积的最大值,及此时椭圆的方程.
,求△AOB面积的最大值,及此时椭圆的方程.
【答案】解:设A(x1,y1),B(x2,y2),
(Ⅰ)由 ![]() 得4x2+2x+1﹣a=0,
得4x2+2x+1﹣a=0,
则x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
则|AB|= ![]() =
= ![]() ,解得a=2.
,解得a=2.
(Ⅱ)由 ![]() ,得(3+k2)x2+2kx+1﹣a=0,
,得(3+k2)x2+2kx+1﹣a=0,
则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
由 ![]() =2
=2 ![]() 得(﹣x1,1﹣y1)=2(x2,y2﹣1),
得(﹣x1,1﹣y1)=2(x2,y2﹣1),
解得x1=﹣2x2,代入上式得:
x1+x2=﹣x2=﹣ ![]() ,则x2=
,则x2= ![]() ,
,
![]() =
= ![]() =
= ![]() ,
,
当且仅当k2=3时取等号,此时x2= ![]() ,x1x2=﹣2x22=﹣2×
,x1x2=﹣2x22=﹣2× ![]() ,
,
又x1x2= ![]() =
= ![]() ,
,
则 ![]() =﹣
=﹣ ![]() ,解得a=5.
,解得a=5.
所以,△AOB面积的最大值为 ![]() ,此时椭圆的方程为3x2+y2=5
,此时椭圆的方程为3x2+y2=5
【解析】(1)本小题的关键是线段AB长的表示,求得过程为![]() ;(2)本题关键在于三角形AOB面积的表示,求得过程为:S△AOB=
;(2)本题关键在于三角形AOB面积的表示,求得过程为:S△AOB=![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某射击运动员每次击中目标的概率都是0.7.现采用随机模拟的方法估计该运动员射击4次,至少击中2次的概率:先由计算器算出0~9之间取整数值的随机数,指定0,1,2表示没有击中目标,3,4,5,6,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:
5727 0293 7140 9857 0347
4373 8636 9647 1417 4698
0371 6233 2616 8045 6011
3661 9597 7424 6710 4281
据此估计,该射击运动员射击4次至少击中2次的概率为( )
A. 0.8 B. 0.85 C. 0.9 D. 0.95
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个关于圆锥曲线的命题中:
①双曲线 ![]() 与椭圆
与椭圆 ![]() 有相同的焦点;
有相同的焦点;
②以抛物线的焦点弦(过焦点的直线截抛物线所得的线段)为直径的圆与抛物线的准线是相切的;
③设A、B为两个定点,k为常数,若|PA|﹣|PB|=k,则动点P的轨迹为双曲线;
④过定圆C上一点A作圆的动弦AB,O为原点,若 ![]() 则动点P的轨迹为椭圆.其中正确的个数是( )
则动点P的轨迹为椭圆.其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个体服装店经营某种服装,在某周内获得的纯利润y(单位:元)与该周每天销售这种服装的件数x之间的一组数据关系如下表:
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求纯利润y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装20件,估计可获得纯利润多少元?
已知:![]() =280,
=280,![]() xiyi=3 487,
xiyi=3 487,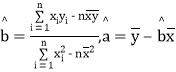 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l1 , l2分别过点A(3 ![]() ,2),B(
,2),B( ![]() ,6),它们分别绕点A,B旋转,但始终保持l1⊥l2 . 若l1与l2的交点为P,坐标原点为O,则线段OP长度的取值范围是( )
,6),它们分别绕点A,B旋转,但始终保持l1⊥l2 . 若l1与l2的交点为P,坐标原点为O,则线段OP长度的取值范围是( )
A.[3,9]
B.[3,6]
C.[6,9]
D.[9,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三点A(1,2),B(﹣3,0),C(3,﹣2).
(1)求证△ABC为等腰直角三角形;
(2)若直线3x﹣y=0上存在一点P,使得△PAC面积与△PAB面积相等,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x2﹣2x﹣8≤0,q:x2+mx﹣6m2≤0,m>0.
(1)若q是p的必要不充分条件,求m的取值范围;
(2)若p是q的充分不必要条件,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x/元 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y/件 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求线性回归方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =-20,
=-20, ![]() =
=![]() -
-![]()
![]() .
.
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com