练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知$\overrightarrow{MN}=\overrightarrow a+5\overrightarrow b$，$\overrightarrow{NP}=-2（\overrightarrow a-4\overrightarrow b）$，$\overrightarrow{PQ}=3（\overrightarrow a-\overrightarrow b）$，则（　　）
    A．M，N，P三点共线B．M，N，Q三点共线C．M，P，Q三点共线D．N，P，Q三点共线

    分析 利用向量共线定理即可判断出结论．

    解答 解：$\overrightarrow{NQ}$=$\overrightarrow{NP}+\overrightarrow{PQ}$=$\overrightarrow{a}$+5$\overrightarrow{b}$=$\overrightarrow{MN}$，
    ∴M，N，Q三点共线．
    故选：B．

    点评 本题考查了向量共线定理，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=lnx-ax-1（a∈R），g（x）=xf（x）+$\frac{1}{2}{x^2}$+2x．
    （Ⅰ）求f（x）的单调区间；
    （Ⅱ）当a=1时，若函数g（x）在区间（m，m+1）（m∈Z）内存在唯一的极值点，求m的值．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年陕西省高一下学期期末考数学试卷（解析版） 题型：选择题

    的值为

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年江西省南昌市高二文下学期期末考试数学试卷（解析版） 题型：选择题

    已知函数y=f（x）在R上为奇函数，且当x≥0时，f（x）=x2﹣2x，则当x＜0时，f（x）的解析式是（ ）

    A．f（x）=﹣x（x+2） B．f（x）=x（x﹣2）

    C．f（x）=﹣x（x﹣2） D．f（x）=x（x+2）

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年江西省南昌市高一下学期期末考试数学试卷（解析版） 题型：解答题

    已知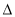ABC的三边为a,b,c．其面积S= 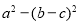,且b+c=8．

    （1）求cosA

    （2）求S的最大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=ex-k-x，（x∈R）
    （1）当k=0时，若函数f（x）≥m在R上恒成立，求实数m的取值范围；
    （2）试判断当k＞1时，函数f（x）在（k，2k）内是否存在零点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数y=f（x）（x≠0）是奇函数，且当x∈（0，+∞）时是增函数，若f（-1）=0，$f（a-\frac{1}{2}）＜0$，
    （1）求f（1）的值；
    （2）求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若函数f（x）=loga（x3-2x）（a＞0且a≠1）在区间（-$\sqrt{2}$，-1）内恒有f（x）＞0，则f（x）的单调递减区间为（　　）
    A．（-∞，-$\frac{\sqrt{6}}{3}$），（$\frac{\sqrt{6}}{3}$，+∞）B．（-$\sqrt{2}$，-$\frac{\sqrt{6}}{3}$），（$\sqrt{2}$，+∞）C．（-$\sqrt{2}$，-$\frac{\sqrt{6}}{3}$），（$\frac{\sqrt{6}}{3}$，+∞）D．（-$\frac{\sqrt{6}}{3}$，$\frac{\sqrt{6}}{3}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．由下列各组命题构成的新命题“p且q”为真命题的是（　　）
    A．p：4+4=9，q：7＞4B．p：a∈{a，b，c}，q：{a}⊆{a，b，c}
    C．p：15是质数，q：8是12的约数D．p：2是偶数，q：2不是质数

    查看答案和解析>>

    同步练习册答案