
| A. | (-∞,-4] | B. | (-$\frac{1}{2}$,+∞) | C. | (-∞,-$\frac{9}{8}$) | D. | (-∞,$\frac{10}{7}$) |
分析 判断函数f(x)的单调性,利用函数与方程之间的关系转化为两个函数图象问题,利用数形结合进行求解即可.
解答  解:对于任意x∈[1,3],不等式f(x)>|x-2|+m恒成立,
解:对于任意x∈[1,3],不等式f(x)>|x-2|+m恒成立,
则等价为对于任意x∈[1,3],不等式$\frac{{2}^{x+1}+1}{{2}^{x}-1}$>|x-2|+m恒成立,
f(x)=$\frac{{2}^{x+1}+1}{{2}^{x}-1}$=$\frac{2({2}^{x}-1)+3}{{2}^{x}-1}$=2+$\frac{3}{{2}^{x}-1}$,
则函数f(x)在x∈[1,3]上为减函数,
故最小值为f(3)=$\frac{{2}^{4}+1}{{2}^{3}-1}$=$\frac{17}{7}$,
设g(x)=|x-2|+m,
则g(x)关于x=2对称,
作出f(x)和g(x)的图象如图,
要使f(x)>|x-2|+m恒成立,
则只需要当x=3时 f(3)>|3-2|+m恒成立即可,
即$\frac{17}{7}$>1+m,
则m<$\frac{17}{7}$-1=$\frac{10}{7}$,
故m<$\frac{10}{7}$,
故选:D.
点评 本题主要考查不等式恒成立问题,利用函数与方程的关系,转化为两个函数的大小问题,利用数形结合是解决本题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
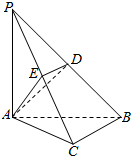 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com