
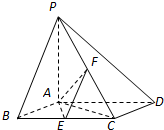
 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.分析 (1)推导出AE⊥BC,AE⊥AD,PA⊥AE,从而AE⊥平面PAD,由此能证明AE⊥PD.
(2)设AB=2,H为PD上任意一点,连接AH,EH,∠EHA为EH与平面PAD所成的角,推导出∠ADH=45°,所以PA=2.
法一:过E作EO⊥AC于O,则EO⊥平面PAC,过O作OS⊥AF于S,连接ES,则∠ESO为二面角E-AF-C的平面角,由此能求出二面角E-AF-C的余弦值.
法二:由AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,利用向量法能求出二面角E-AF-C的余弦值.
法三:建立空间直角坐标系,设菱形ABCD的边长为2,设P(0,0,t)(t>0),利用向量法能求出二面角E-AF-C的余弦值.
解答 证明:(1)由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC
又BC∥AD,因此AE⊥AD
因为PA⊥平面ABCD,AE?平面ABCD,所以PA⊥AE
而PA?平面PAD,AD?平面PAD且PA∩AD=A
所以AE⊥平面PAD.又PD?平面PAD
所以AE⊥PD.(3分)
解:(2)设AB=2,H为PD上任意一点,连接AH,EH.
由(1)知AE⊥平面PAD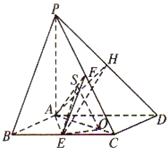
所以∠EHA为EH与平面PAD所成的角
在Rt△EAH中,$AE=\sqrt{3}$,
所以当AH最短时,∠EHA最大,即当AH⊥PD时,∠EHA最大.
因为$sin∠EHA=\frac{{\sqrt{15}}}{5}$,此时$tan∠EHA=\frac{AE}{AH}=\frac{{\sqrt{3}}}{AH}=\frac{{\sqrt{6}}}{2}$
因此$AH=\sqrt{2}$.又AD=2,所以∠ADH=45°,所以PA=2.(5分)
解法一:因为PA⊥平面ABCD,PA?平面PAC
所以平面PAC⊥平面ABCD
过E作EO⊥AC于O,则EO⊥平面PAC
过O作OS⊥AF于S,连接ES,则∠ESO为二面角E-AF-C的平面角,(7分)
在Rt△AOE中,$EO=AE•sin{30°}=\frac{{\sqrt{3}}}{2}$,$AO=AE•cos{30°}=\frac{3}{2}$
又F是PC的中点,在Rt△ASO中,$SO=AO•sin{45°}=\frac{{3\sqrt{2}}}{4}$
又$SE=\sqrt{E{O^2}+S{O^2}}=\sqrt{\frac{3}{4}+\frac{9}{8}}=\frac{{\sqrt{30}}}{4}$
在Rt△ESO中,$cos∠ESO=\frac{SO}{SE}=\frac{{\frac{{3\sqrt{2}}}{4}}}{{\frac{{\sqrt{30}}}{4}}}=\frac{{\sqrt{15}}}{5}$,(9分)
即所求二面角的余弦值为$\frac{{\sqrt{15}}}{5}$.(10分)
解法二:由(1)知AE,AD,AP两两垂直,
以A为坐标原点,建立如图所示的空间直角坐标系,
又E,F分别为BC,PC的中点,
所以$A(0,0,0),B(\sqrt{3},-1,0),C(\sqrt{3},1,0),D(0,2,0)$$P(0,0,2),E(\sqrt{3},0,0),F({\frac{{\sqrt{3}}}{2},\frac{1}{2},1})$
所以$\overrightarrow{AE}=(\sqrt{3},0,0),\overrightarrow{AF}=({\frac{{\sqrt{3}}}{2},\frac{1}{2},1})$
设平面AEF的一法向量为m=(x1,y1,z1)
则$\left\{\begin{array}{l}m•\overrightarrow{AE}=0\\ m•\overrightarrow{AF}=0\end{array}\right.$因此$\left\{\begin{array}{l}\sqrt{3}{x_1}=0\\ \frac{{\sqrt{3}}}{2}{x_1}+\frac{1}{2}{y_1}+{z_1}=0\end{array}\right.$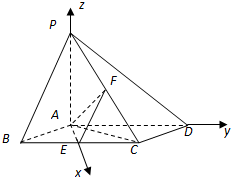
取z1=-1,则m=(0,2,-1),(7分)
因为BD⊥AC,BD⊥PA,PA∩AC=A,所以BD⊥平面AFC
故$\overrightarrow{BD}$为平面AFC的一法向量,又$\overrightarrow{BD}=(-\sqrt{3},3,0)$
所以$cos<m,\overrightarrow{BD}>=\frac{{m•\overrightarrow{BD}}}{{|m|•|{\overrightarrow{BD}}|}}=\frac{2×3}{{\sqrt{5}×\sqrt{12}}}=\frac{{\sqrt{15}}}{5}$.(9分)
因为二面角E-AF-C为锐角,所以所求二面角的余弦值为$\frac{{\sqrt{15}}}{5}$.(10分)
解法三:建立如图所示的空间直角坐标系,
设菱形ABCD的边长为2,则$A({0,0,0}),E({\sqrt{3},0,0}),D({0,2,0}),C({\sqrt{3},1,0})$,
设P(0,0,t)(t>0)
由P,H,D三点共线可设$\overrightarrow{DH}=λ\overrightarrow{DP}(0≤λ≤1)$,则H(0,2-2λ,λt),(4分)
∴$\overrightarrow{EH}=({-\sqrt{3},2-2λ,λt})$,又平面PAD的一个法向量$\overrightarrow n=({1,0,0})$
设EH与平面PAD所成角为θ,则$sinθ=|{cos<\overrightarrow{EH},\overrightarrow n>}|=\frac{{\sqrt{3}}}{{\sqrt{{λ^2}{t^2}+4{{(λ-1)}^2}+3}}}$-(5分)
令g(λ)=λ2t2+4(λ-1)2+3=(4+t2)λ2-8λ+7(0≤λ≤1)
∴$当λ=\frac{4}{{4+{t^2}}}∈[{0,1}]时,g{(λ)_{min}}=\frac{{7{t^2}+12}}{{4+{t^2}}}(t>0)$(6分)
∴${(sinθ)_{max}}=\frac{{\sqrt{3}}}{{\sqrt{\frac{{7{t^2}+12}}{{4+{t^2}}}}}}\frac{{\sqrt{15}}}{5},解得t=2,即P({0,0,2}),则F({\frac{{\sqrt{3}}}{2},\frac{1}{2},1})$,(7分)
∴$\overline{AE}=({\sqrt{3},0,0}),\overrightarrow{AF}=({\frac{{\sqrt{3}}}{2},\frac{1}{2},1}),\overrightarrow{AC}=({\sqrt{3},1,0})$,
设平面AEF的法向量$\overrightarrow{{n}_{1}}$=(x,y,z),
则$\left\{\begin{array}{l}{{\overrightarrow{{n}_{1}}•\overrightarrow{AE}=\sqrt{3}x=0}_{\;}}\\{\overrightarrow{{n}_{1}}•\overrightarrow{AF}=\frac{\sqrt{3}}{2}x+\frac{1}{2}y+z=0}\end{array}\right.$,取y=2,得$\overrightarrow{n_1}=({0,2,-1})$,
设平面AFC的一个法向量$\overrightarrow{{n}_{2}}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}•\overrightarrow{AC}=\sqrt{3}a+b=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{AF}=\frac{\sqrt{3}}{2}a+\frac{1}{2}b+c=0}\end{array}\right.$,取a=1,得$\overrightarrow{n_2}=({1,-\sqrt{3},0})$-(8分)
∴$cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{-2\sqrt{3}}}{{\sqrt{5}×2}}=-\frac{{\sqrt{15}}}{5}$,(9分)
又∵二面角E-AF-C是锐二面角
∴二面角E-AF-C的余弦值为$\frac{\sqrt{15}}{5}$.(10分)
点评 本题考查线线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 0 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点
如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=$\frac{π}{3}$,AD=4,AM=2,E是AB的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 出生时间 性别 | 晚上 | 白天 | 合计 |
| 男婴 | |||
| 女婴 | |||
| 合计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com