
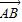 ,
,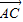 ,然后求出平面ABC的一个法向量,通过法向量与
,然后求出平面ABC的一个法向量,通过法向量与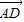 的数量积即可求出顶点D到平面ABC的距离.
的数量积即可求出顶点D到平面ABC的距离.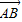 =(2,-2,-3),
=(2,-2,-3),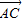 =(3,0,6),
=(3,0,6),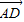 =(-7,-7,7).
=(-7,-7,7).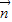 =(a,b,c)
=(a,b,c)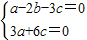 ,不妨令a=4,则c=-2,解得b=5.
,不妨令a=4,则c=-2,解得b=5.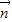 =(4,5,-2).
=(4,5,-2).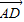 在平面ABC的法向量投影的长度,即:
在平面ABC的法向量投影的长度,即: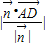 =
=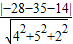 =11.
=11.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2010年吉林省高考复习质量检测数学试卷(理科)(解析版) 题型:选择题



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com