【题目】设双曲线
的左右焦点分别为
，过
的直线分别交双曲线左右两支于点M，N.若以MN为直径的圆经过点
且
，则双曲线的离心率为（ ）
A.
B.
C.
D.
应用题天天练四川大学出版社系列答案科目：高中数学 来源： 题型：
【题目】已知极点为直角坐标系的原点，极轴为
轴正半轴且单位长度相同的极坐标系中曲线
，
（
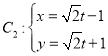为参数）.
（Ⅰ）求曲线
上的点到曲线
距离的最小值；
（Ⅱ）若把上各点的横坐标都扩大原来为原来的2倍，纵坐标扩大原来的
倍，得到曲线
，设
，曲线与交于
，
两点，求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
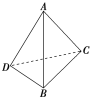
【题目】如图，在三棱锥A-BCD中，AD⊥BD，AC⊥BC，∠DAB＝
，∠BAC＝
.三棱锥的外接球的表面积为16π，则该三棱锥的体积的最大值为( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是某小区2017年1月至2018年1月当月在售二手房均价（单位：万元/平方米）的散点图.（图中月份代码1—13分别对应2017年1月—2018年1月）
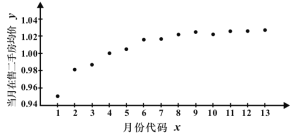
由散点图选择
和
两个模型进行拟合，经过数据处理得到两个回归方程分别为
和
，并得到以下一些统计量的值：
|
| |
残差平方和 | 0.000591 | 0.000164 |
总偏差平方和 | 0.006050 | |
（1）请利用相关指数
判断哪个模型的拟合效果更好；
（2）某位购房者拟于2018年6月份购买这个小区
平方米的二手房（欲
购房为其家庭首套房）.若购房时该小区所有住房的房产证均已满2年但未满5年，请你利用（1）中拟合效果更好的模型估算该购房者应支付的购房金额.（购房金额=房款+税费；房屋均价精确到0.001万元/平方米）
附注：根据有关规定，二手房交易需要缴纳若干项税费，税费是按房屋的计税价格进行征收.（计税价格=房款），征收方式见下表：
契税 （买方缴纳） | 首套面积90平方米以内（含90平方米）为1%；首套面积90平方米以上且144平方米以内（含144平方米）为1.5%；面积144平方米以上或非首套为3% |
增值税 （卖方缴纳） | 房产证未满2年或满2年且面积在144平方米以上（不含144平方米）为5.6%；其他情况免征 |
个人所得税 （卖方缴纳） | 首套面积144平方米以内（含144平方米）为1%；面积144平方米以上或非首套均为1.5%；房产证满5年且是家庭唯一住房的免征 |
参考数据：
，
，
，
，
，
，
，
. 参考公式：相关指数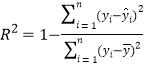
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地有两个国家AAAA级景区—甲景区和乙景区.相关部门统计了这两个景区2019年1月至6月的客流量（单位：百人），得到如图所示的茎叶图.关于2019年1月至6月这两个景区的客流量，下列结论正确的是（ ）
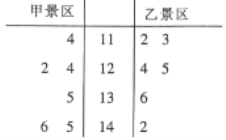
A.甲景区客流量的中位数为13000
B.乙景区客流量的中位数为13000
C.甲景区客流量的平均值比乙景区客流量的平均值小
D.甲景区客流量的极差比乙景区客流量的极差大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
