
【题目】在![]() 年俄罗斯索契冬奥会某项目的选拔比赛中,
年俄罗斯索契冬奥会某项目的选拔比赛中,![]() 、
、![]() 两个代表队进行对抗赛,每队三名队员,
两个代表队进行对抗赛,每队三名队员,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,
,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得
,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得![]() 分,负队得
分,负队得![]() 分,设
分,设![]() 队、
队、![]() 队最后所得总分分别为
队最后所得总分分别为![]() 、
、![]() 且
且![]() .
.
对阵队员 |
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 队得分为
队得分为![]() 分的概率;
分的概率;
(2)求![]() 的分布列;并用统计学的知识说明哪个队实力较强.
的分布列;并用统计学的知识说明哪个队实力较强.
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的圆心坐标为(1,0),半径为1.
(1)求圆C的极坐标方程;
(2)若以极点O为原点,极轴所在直线为x轴建立平面直角坐标系.已知直线l的参数方程为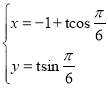 (t为参数),试判断直线l与圆C的位置关系.
(t为参数),试判断直线l与圆C的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生参加4门学科的学业水平测试,每门得![]() 等级的概率都是
等级的概率都是![]() ,该学生各学科等级成绩彼此独立.规定:有一门学科获
,该学生各学科等级成绩彼此独立.规定:有一门学科获![]() 等级加1分,有两门学科获
等级加1分,有两门学科获![]() 等级加2分,有三门学科获
等级加2分,有三门学科获![]() 等级加3分,四门学科全获
等级加3分,四门学科全获![]() 等级则加5分,记
等级则加5分,记![]() 表示该生的加分数,
表示该生的加分数, ![]() 表示该生获
表示该生获![]() 等级的学科门数与未获
等级的学科门数与未获![]() 等级学科门数的差的绝对值.
等级学科门数的差的绝对值.
(1)求![]() 的数学期望;
的数学期望;
(2)求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .记点
.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上的动点,且直线
上的动点,且直线![]() 过点
过点![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,请求出定点
?若存在,请求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着社会发展对环保的要求,越来越多的燃油汽车被电动汽车取代,为了了解某品牌的电动汽车的节能情况,对某一辆电动汽车“行车数据”的两次记录如下表:
记录时间 | 累计里程 (单位:公里) | 平均耗电量(单位: | 剩余续航里程 (单位:公里) |
2020年1月1日 | 5000 | 0.125 | 380 |
2020年1月2日 | 5100 | 0.126 | 246 |
(注:累计里程指汽车从出厂开始累计行驶的路程,累计耗电量指汽车从出厂开始累计消耗的电量,![]()
![]() )
)
下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是( )
A.等于![]() B.
B.![]() 到
到![]() 之间C.等于
之间C.等于![]() D.大于
D.大于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点![]() 的横、纵坐标分别为第
的横、纵坐标分别为第![]() 名工人上午的工作时间和加工的零件数,点
名工人上午的工作时间和加工的零件数,点![]() 的横、纵坐标分别为第
的横、纵坐标分别为第![]() 名工人下午的工作时间和加工的零件数,
名工人下午的工作时间和加工的零件数,![]() .记
.记![]() 为第
为第![]() 名工人在这一天中加工的零件总数,记
名工人在这一天中加工的零件总数,记![]() 为第
为第![]() 名工人在这一天中平均加工的零件数,则
名工人在这一天中平均加工的零件数,则![]() ,
,![]() ,
,![]() 中的最大值与
中的最大值与![]() ,
,![]() ,
,![]() 中的最大值分别是( )
中的最大值分别是( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上7:00至7:15之间到某公交站搭乘公交车去上学,已知在这段时间内,共有2班公交车到达该站,到站的时间分别为7:05,7:15,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
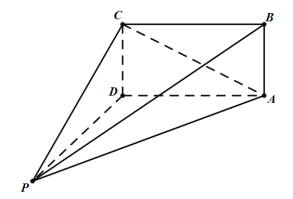
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,底面
,底面![]() 为正方形,且
为正方形,且![]() .若四棱锥
.若四棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,则球
的球面上,则球![]() 的表面积的最小值为_____;当四棱锥
的表面积的最小值为_____;当四棱锥![]() 的体积取得最大值时,二面角
的体积取得最大值时,二面角![]() 的正切值为_______.
的正切值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com