
【题目】正三棱台的上、下底面的边长分别是3和6. 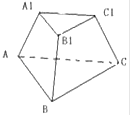
(1)若侧面与底面所成的角为60°,求此三棱台的体积;
(2)若侧棱与底面所成的角为60°,求此三棱台的侧面积.
【答案】
(1)解:如图,
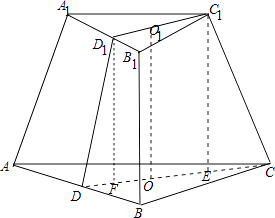
作C1D1⊥A1B1,CD⊥AB,作C1E⊥CD=E,D1F⊥CD=F,
∵上底面边长为3,∴上底面边A1B1上的高 ![]() ,
,
则 ![]() ,
,
∵下底面边长为6,∴下底面边AB上的高为CD= ![]() ,
,
则 ![]() ,
,
∴ ![]() ,
, ![]() ,
,
上底面面积为 ![]() ,下底面面积为
,下底面面积为 ![]() .
.
若正三棱台侧面与底面成60°,即∠D1DF=60°,
∴三棱台的高为 ![]() ,
,
则三棱台体积V= ![]() =
= ![]()
(2)解:若正三棱台侧棱与底面成60°,即∠C1CE=60°,
∴三棱台的高为 ![]() ,
,
则三棱台的斜高为 ![]() ,
,
∴此三棱台的侧面积为3× ![]()
【解析】由题意画出图形,由已知求出上下底面面积.(1)当侧面与底面所成的角为60°时,解三角形求出棱台的高,代入体积公式得答案;(2)当侧棱与底面所成的角为60°时,解三角形求出棱台的斜高,代入侧面积公式得答案.


科目:高中数学 来源: 题型:
【题目】为提高市场销售业绩,某公司设计两套产品促销方案(方案1运作费用为![]() 元/件;方案2的的运作费用为
元/件;方案2的的运作费用为![]() 元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如下表所示.
元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如下表所示.
无促销活动 | 采用促销方案1 | 采用促销方案2 | ||
本年度平均销售额不高于上一年度平均销售额 | 48 | 11 | 31 | 90 |
本年度平均销售额高于上一年度平均销售额 | 52 | 69 | 29 | 150 |
100 | 80 | 60 |
(Ⅰ)请根据列联表提供的信息,为该公司今年选择一套较为有利的促销方案(不必说明理由);
(Ⅱ)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的![]() 组售价
组售价![]() (单位:元/件,整数)和销量
(单位:元/件,整数)和销量![]() (单位:件)(
(单位:件)(![]() )如下表所示:
)如下表所示:
售价 |
|
|
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
|
|
(ⅰ)请根据下列数据计算相应的相关指数![]() ,并根据计算结果,选择合适的回归模型进行拟合;
,并根据计算结果,选择合适的回归模型进行拟合;
(ⅱ)根据所选回归模型,分析售价![]() 定为多少时?利润
定为多少时?利润![]() 可以达到最大.
可以达到最大.
|
|
| |
|
|
|
|
|
| ||
参考公式:相关指数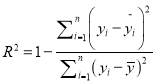 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义平面向量之间的一种运算“⊙”如下:对任意的 ![]() ,令
,令 ![]() ,下面说法错误的是( )
,下面说法错误的是( )
A.若 ![]() 与
与 ![]() 共线,则
共线,则 ![]() ⊙
⊙ ![]() =0
=0
B.![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]()
C.对任意的λ∈R,有 ![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]() )
)
D.( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=|
)2=| ![]() |2|
|2| ![]() |2
|2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
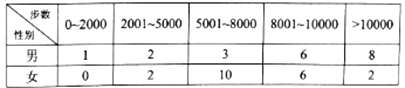
(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
 附:
附:  ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,圆
轴的正半轴,两种坐标系中的长度单位相同,圆![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),射线
为参数),射线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +
+ ![]()
(1)将函数f(x)化简成Asin(ωx+φ)+B(A>0,φ>0,φ∈[0,2π))的形式;
(2)求f(x)的单调递减区间,并指出函数|f(x)|的最小正周期;
(3)求函数f(x)在[ ![]() ,
, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有A,B,C三家社区医院,并且他们的选择是相互独立的.
(Ⅰ)求甲、乙两人都选择A社区医院的概率;
(Ⅱ)求甲、乙两人不选择同一家社区医院的概率;
(Ⅲ)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com