
【题目】已知函数f(x)=k(x﹣1)ex+x2 . (Ⅰ)当时k=﹣ ![]() ,求函数f(x)在点(1,1)处的切线方程;
,求函数f(x)在点(1,1)处的切线方程;
(Ⅱ)若在y轴的左侧,函数g(x)=x2+(k+2)x的图象恒在f(x)的导函数f′(x)图象的上方,求k的取值范围;
(Ⅲ)当k≤﹣l时,求函数f(x)在[k,1]上的最小值m.
【答案】解:(Ⅰ)k=﹣ ![]() 时,f(x)=﹣
时,f(x)=﹣ ![]() (x﹣1)ex+x2,
(x﹣1)ex+x2,
∴f′(x)=x(2﹣ex﹣1 ),∴f′(1)=1,f(1)=1,
∴函数f(x)在(1,1)处的切线方程为y=x,
(Ⅱ)f′(x)=kx(ex+ ![]() )<x2+(k+2)x,
)<x2+(k+2)x,
即:kxex﹣x2﹣kx<0,
∵x<0,∴kex﹣x﹣k>0,
令h(x)=kex﹣x﹣k,
∴h′(x)=kex﹣1,
当k≤0时,h(x)在x<0时递减,h(x)>h(0)=0,符合题意,
当0<k≤1时,h(x)在x<0时递减,h(x)>h(0)=0,符合题意,
当k>1时,h(x)在(﹣∞,﹣lnk)递减,在(﹣lnk,0)递增,
∴h(﹣lnk)<h(0)=0,不合题意,
综上:k≤1.
(Ⅲ)f′(x)=kx(ex+ ![]() ),
),
令f′(x)=0,解得:x1=0,x2=ln(﹣ ![]() ),
),
令g(k)=ln(﹣ ![]() )﹣k,则g′(k)=﹣
)﹣k,则g′(k)=﹣ ![]() ﹣1≤0,
﹣1≤0,
g(k)在k=﹣1时取最小值g(﹣1)=1+ln2>0,
∴x2=ln(﹣ ![]() )>k,
)>k,
当﹣2<k≤﹣1时,x2=ln(﹣ ![]() )>0,
)>0,
f(x)的最小值为m=min{f(0),f(1)}=min{﹣k,1}=1,
当k=﹣2时,函数f(x)在区间[k,1]上递减,m=f(10=1,
当k<﹣2时,f(x)的最小值为m=min{f(x2 ),f(1)},
f(x2 )=﹣2[ln(﹣ ![]() )﹣1]+[ln(﹣
)﹣1]+[ln(﹣ ![]() )]2=
)]2= ![]() ﹣2x2+2>1,f(1)=1,
﹣2x2+2>1,f(1)=1,
此时m=1,
综上:m=1.
【解析】(Ⅰ)k=﹣ ![]() 时,f(x)=﹣
时,f(x)=﹣ ![]() (x﹣1)ex+x2,得f′(x)=x(2﹣ex﹣1 ),从而求出函数f(x)在(1,1)处的切线方程;(Ⅱ)f′(x)=kx(ex+
(x﹣1)ex+x2,得f′(x)=x(2﹣ex﹣1 ),从而求出函数f(x)在(1,1)处的切线方程;(Ⅱ)f′(x)=kx(ex+ ![]() )<x2+(k+2)x,即:kxex﹣x2﹣kx<0,令h(x)=kex﹣x﹣k,讨论当k≤0时,当0<k≤1时,当k>1时,从而综合得出k的范围;(Ⅲ)f′(x)=kx(ex+
)<x2+(k+2)x,即:kxex﹣x2﹣kx<0,令h(x)=kex﹣x﹣k,讨论当k≤0时,当0<k≤1时,当k>1时,从而综合得出k的范围;(Ⅲ)f′(x)=kx(ex+ ![]() ),令f′(x)=0,得:x1=0,x2=ln(﹣
),令f′(x)=0,得:x1=0,x2=ln(﹣ ![]() ),令g(k)=ln(﹣
),令g(k)=ln(﹣ ![]() )﹣k,则g′(k)=﹣
)﹣k,则g′(k)=﹣ ![]() ﹣1≤0,得g(k)在k=﹣1时取最小值g(﹣1)=1+ln2>0,讨论当﹣2<k≤﹣1时,当k=﹣2时,当k<﹣2时的情况,从而求出m的值.
﹣1≤0,得g(k)在k=﹣1时取最小值g(﹣1)=1+ln2>0,讨论当﹣2<k≤﹣1时,当k=﹣2时,当k<﹣2时的情况,从而求出m的值.
【考点精析】通过灵活运用函数的最大(小)值与导数,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,PA⊥☉O所在的平面,AB是☉O的直径,C是☉O上的一点,AE⊥PB于E,AF⊥PC于F,给出下列结论:①BC⊥平面PAC;②AF⊥平面PCB;③EF⊥PB;④AE⊥平面PBC.其中正确命题的个数是( )
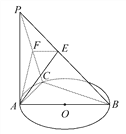
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是甲、乙两人在一次射击比赛中中靶的情况(击中靶中心的圆面为10环,靶中各数字表示该数字所在圆环被击中所得的环数),每人射击了6次.
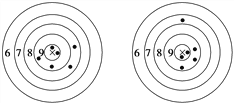
甲射击的靶 乙射击的靶
(1)请用列表法将甲、乙两人的射击成绩统计出来;
(2)请你用学过的统计知识,对甲、乙两人这次的射击情况进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() 是定义在[-l,1]上的奇函数,且f(
是定义在[-l,1]上的奇函数,且f(![]() )=
)=![]() 。
。
(1)确定函数f(x)的解析式;
(2)判断并用定义证明f(x)在(-1,1)上的单调性;
(3)若f(1-3m)+f(1+m)≥0,求实数m的所有可能的取值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过
不超过![]() 尾/立方米时,
尾/立方米时, ![]() 的值为
的值为![]() 千克/年;当
千克/年;当![]() 时,
时, ![]() 是
是![]() 的一次函数,且当
的一次函数,且当![]() 时,
时, ![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 关于
关于![]() 的函数的表达式.
的函数的表达式.
(![]() )当养殖密度
)当养殖密度![]() 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(其中A>0,ω>0,0<φ<
,(其中A>0,ω>0,0<φ<![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为![]() ,且图象上一个最低点为M(
,且图象上一个最低点为M(![]() ,-2).
,-2).
(1)求f(x)的解析式;
(2)将函数f(x)的图象向右平移![]() 个单位后,再将所得图象上各点的横坐标缩小到原来的
个单位后,再将所得图象上各点的横坐标缩小到原来的![]() ,纵坐标不变,得到y=g(x)的图象,求函数y=g(x)的解析式.
,纵坐标不变,得到y=g(x)的图象,求函数y=g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xex , 则( )
A.x=1为f(x)的极大值点
B.x=1为f(x)的极小值点
C.x=﹣1为f(x)的极大值点
D.x=﹣1为f(x)的极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公共汽车线路收支差额(票价总收人减去运营成本)与乘客量的函数图象.目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会.乘客代表认为:公交公司应节约能源,改善管理,降低运营成本,以此举实现扭亏.公交公司认为:运营成本难以下降,公司己尽力,提高票价才能扭亏.根据这两种意见,可以把图分别改画成图②和图③,
(1)说明图①中点![]() 和点
和点![]() 以及射线
以及射线![]() 的实际意义;
的实际意义;
(2)你认为图②和图③两个图象中,反映乘客意见的是_________,反映公交公司意见的是_________.
(3)如果公交公司采用适当提高票价又减少成本的办法实现扭亏为赢,请你在图④中画出符合这种办法的大致函数关系图象.
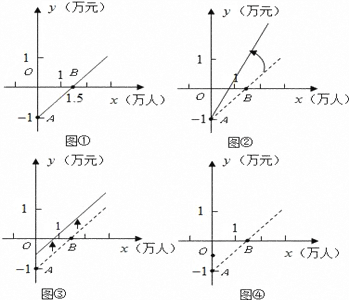
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() ,其中函数f(x)的图象在点(1,f(1))处的切线方程为y=x﹣1.
,其中函数f(x)的图象在点(1,f(1))处的切线方程为y=x﹣1.
(1)若a= ![]() ,求函数f(x)的解析式;
,求函数f(x)的解析式;
(2)若f(x)≥g(x)在[1,+∞)上恒成立,求实数a的取值范围;
(3)证明:1+ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com