
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)问:![]() 的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
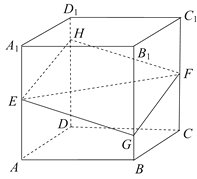
【题目】如图,正方体![]() 的棱长为
的棱长为![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过点
的中点,过点![]() 的平面分别与棱
的平面分别与棱![]() ,
,![]() 交于点
交于点![]() ,设
,设![]() .给出以下四个命题:
.给出以下四个命题:
①平面![]() 与平面
与平面![]() 所成角的最大值为45°;
所成角的最大值为45°;
②四边形![]() 的面积的最小值为
的面积的最小值为![]() ;
;
③四棱锥![]() 的体积为
的体积为![]() ;
;
④点![]() 到平面
到平面![]() 的距离的最大值为
的距离的最大值为![]() .
.
其中命题正确的序号为( )
A.②③④B.②③C.①②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】最近,纪录片《美国工厂》引起中美观众热议,大家都认识到,大力发展制造业,是国家强盛的基础,而产业工人的年龄老化成为阻碍美国制造业发展的障碍,中国应未雨绸缪.某工厂有35周岁以上(含35周岁)工人300名,35周岁以下工人200名,为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“35周岁以上(含35周岁)”和“35周岁以下”分为两组,在将两组工人的日平均生产件数分成5组:![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
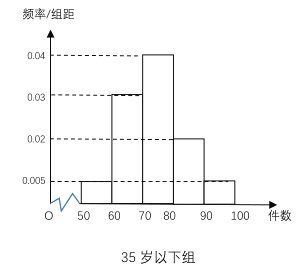
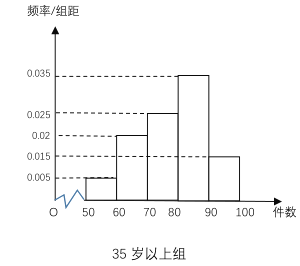
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“35周岁以下组”工人的概率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成![]() 的列联表,并判断是否有95%的把握认为“生产能手与工人所在的年龄组有关”?
的列联表,并判断是否有95%的把握认为“生产能手与工人所在的年龄组有关”?
生产能手 | 非生产能手 | 合计 | |
35岁以下 | |||
35岁以上 | |||
合计 |
附表: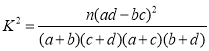
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图,下列描述正确的是( ).
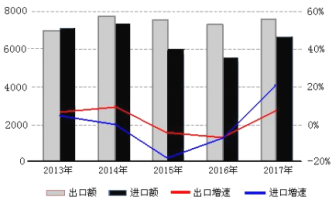
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,卷一《方田》中有如下两个问题:
[三三]今有宛田,下周三十步,径十六步.问为田几何?
[三四]又有宛田,下周九十九步,径五十一步.问为田几何?
翻译为:[三三]现有扇形田,弧长30步,直径长16步.问这块田面积是多少?
[三四]又有一扇形田,弧长99步,直径长51步.问这块田面积是多少?
则下列说法正确的是( )
A.问题[三三]中扇形的面积为240平方步B.问题[三四]中扇形的面积为![]() 平方步
平方步
C.问题[三三]中扇形的面积为60平方步D.问题[三四]中扇形的面积为![]() 平方步
平方步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 与
与![]() 轴交于
轴交于![]() 两点.以坐标原点
两点.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 在第一象限交于点
在第一象限交于点![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.
是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.

(Ⅰ)求证:PO平面![]() ;
;
(Ⅱ)求平面EFG与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,若存在,求线段
,若存在,求线段![]() 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由n(n∈N*)个正整数构成的集合A={a1,a2,…,an}(a1<a2<…<an,n≥3),记SA=a1+a2+…+an,对于任意不大于SA的正整数m,均存在集合A的一个子集,使得该子集的所有元素之和等于m.
(1)求a1,a2的值;
(2)求证:“a1,a2,…,an成等差数列”的充要条件是“![]() ”;
”;
(3)若SA=2020,求n的最小值,并指出n取最小值时an的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com