
【题目】某地计划在水库建一座至多安装3台发电机的水电站.过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台发电机年净利润为5000万元;若某台发电机未运行,则该台发电机年维护费与年入流量![]() 有如下关系:
有如下关系:
年入流量 |
|
|
一台未运行发电机年维护费 | 500 | 800 |
欲使水电站年净利润最大,应安装发电机多少台?
【答案】(1)![]() ;(2)应安装发电机2台.
;(2)应安装发电机2台.
【解析】
(1)由题意求出年入流量![]() 在3个范围:
在3个范围:![]() ,
,![]() ,
,![]() 的概率
的概率![]() .由二项分布可得在未来4年中至多有1年的年入流量超过120的概率;
.由二项分布可得在未来4年中至多有1年的年入流量超过120的概率;
(2)记水电站年净利润为![]() (单位:万元).分别求安装1台发电机、安装2台发电机、安装3台发电机的数学期望
(单位:万元).分别求安装1台发电机、安装2台发电机、安装3台发电机的数学期望![]() ,选择
,选择![]() 最大的方案.
最大的方案.
(1)依题意,![]() ,
,
![]() ,
,![]()
由二项分布,在未来4年中至多有1年的年入流量超过120的概率为:
![]() .
.
(2)记水电站年净利润为![]() (单位:万元)
(单位:万元)
①当安装1台发电机时.
由于水库年入流量总大于40,所以1台发电机运行的概率为1.
此时的年净利润![]() ,
,![]() ;
;
②当安装2台发电机时.此时,
若![]() ,则只有1台发电机运行,此时
,则只有1台发电机运行,此时![]() ,因此
,因此![]()
若![]() ,则2台发电机都能运行,此时
,则2台发电机都能运行,此时![]() ,因此
,因此![]()
由此得![]() 的概率分布列如下:
的概率分布列如下:
| 4500 | 10000 |
| 0.2 | 0.8 |
所以,![]() .
.
③当安装3台发电机时.此时,
若![]() ,则只有1台发电机运行,此时
,则只有1台发电机运行,此时![]() ,因此
,因此![]()
若![]() ,则有2台发电机运行,此时
,则有2台发电机运行,此时![]() ,因此
,因此![]()
若![]() ,则3台发电机同时运行,此时
,则3台发电机同时运行,此时![]() ,因此
,因此![]()
由此得![]() 的概率分布列如下:
的概率分布列如下:
| 4000 | 9200 | 15000 |
| 0.2 | 0.7 | 0.1 |
所以,![]()
综上,欲使水电站年净利润最大,应安装发电机2台.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】十五巧板,又称益智图,为清朝浙江省德清知县童叶庚在同治年间所发明,它能拼出草木、花果、鸟兽、鱼虫、文字等图案.十五巧板由十五块板组成一个大正方形(如图1),其中标号为![]() 的小板为等腰直角三角形,图
的小板为等腰直角三角形,图![]() 是用十五巧板拼出的2019年生肖猪的图案,则从生肖猪图案中任取一点,该点恰好取自阴影部分的概率为( )
是用十五巧板拼出的2019年生肖猪的图案,则从生肖猪图案中任取一点,该点恰好取自阴影部分的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台![]() 中,
中,![]() ,.若点
,.若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 靠近点
靠近点![]() 的四等分点.
的四等分点.
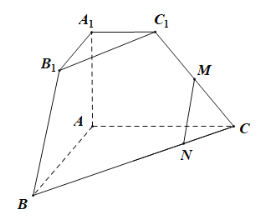
(1)求证:![]() 平面
平面![]() ;
;
(2)若三棱台![]() 的体积为
的体积为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
注:台体体积公式:![]() ,或在
,或在![]() 分别为台体上下底面积,
分别为台体上下底面积,![]() 为台体的高.
为台体的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,平面
的中点,平面![]() 平面
平面![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 平面
平面![]() .
.
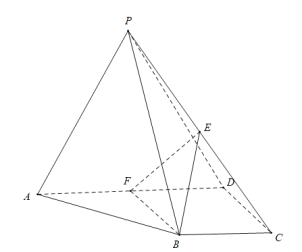
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是衡量空气质量的重要指标,我国采用世卫组织的最宽值限定值,即PM2.5日均值在![]() 以下空气质量为一级,在
以下空气质量为一级,在![]() 空气质量为二级,超过
空气质量为二级,超过![]() 为超标,如图是某地1月1日至10日的PM2.5(单位:
为超标,如图是某地1月1日至10日的PM2.5(单位:![]() )的日均值,则下列说法正确的是( )
)的日均值,则下列说法正确的是( )
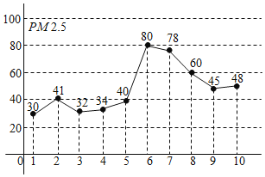
A.10天中PM2.5日均值最低的是1月3日
B.从1日到6日PM2.5日均值逐渐升高
C.这10天中恰有5天空气质量不超标
D.这10天中PM2.5日均值的中位数是43
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且在[0,+∞)上单调递减,f(2)=0,则不等式f(log2x)>0的解集为( )
A.(![]() ,4)B.(2,2)C.(
,4)B.(2,2)C.(![]() ,+∞)D.(4,+∞)
,+∞)D.(4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,平面PAC⊥平面ABCD,且有AB∥DC,AC=CD=DA![]() AB.
AB.

(1)证明:BC⊥PA;
(2)若PA=PC=AC,求平面PAD与平面PBC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)(2017·开封二模)为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率.
(2)检验结束后,甲、乙两名运动员的成绩用茎叶图表示如图:

计算说明哪位运动员的成绩更稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求
,求![]() 的极坐标方程;
的极坐标方程;
(2)若![]() 与
与![]() 恰有4个公共点,求
恰有4个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com