[题目]从4名男生和2名女生中任选3人参加演讲比赛.设随机变量ξ表示所选3人中女生的人数．(1)求所选3人中女生人数ξ≤1的概率, (2)求ξ的分布列及数学期望．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】从4名男生和2名女生中任选3人参加演讲比赛，设随机变量ξ表示所选3人中女生的人数．

（1）求所选3人中女生人数ξ≤1的概率；

（2）求ξ的分布列及数学期望．

【答案】（1）；（2）见解析

【解析】

（1）先求得ξ=2的概率，再利用对立事件的概率公式得到结果．

（2）由题意知ξ服从超几何分布，随机变量ξ表示所选3人中女生的人数，ξ可能的取值为0，1，2，结合变量对应的事件和超几何分布的概率公式，写出变量的分布列和数学期望．

（1）由题意知P(ξ＝2)＝，则“所选3人中女生人数ξ≤1”的概率为.

（2）由题意知ξ服从超几何分布，

随机变量ξ表示所选3人中女生的人数，ξ可能取的值为0，1，2．

．

∴ξ的分布列为

ζ	0	1	2
P

∴ξ的数学期望为

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】设全集U=R，集合A={x|1≤x＜4}，B={x|2a≤x＜3-a}．

（1）若a=-2，求B∩A，B∩(UA)；（2）若A∪B=A，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，圆为圆上任意一点，过作圆的切线，分别交直线和于两点，连接，相交于点，若点的轨迹为曲线.

（1）设直线的斜率分别为，求的值，并求曲线的方程；

（2）记直线与曲线有两个不同的交点，与直线交于点，与直线交于点，求的面积与的面积的比值的最大值及取得最大值时的值.

（注：在点处的切线方程为）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】据统计一次性饮酒4.8两诱发脑血管病的概率为0.04，一次性饮酒7.2两诱发脑血管病的概率为0.16.已知某公司职员一次性饮酒4.8两未诱发脑血管病，则他还能继续饮酒2.4两不诱发脑血管病的概率为（）

A. B. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】从全校参加数学竞赛的学生的试卷中抽取一个样本，考察竞赛的成绩分布情况，将样本分成5组，绘成频率分布直方图，图中从左到右各小长方形的高之比为，最右边一组频数是6，请结合直方图提供的信息，解答下列问题：

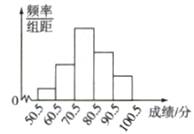
（1）样本量是多少？

（2）列出频率分布表.

（3）估计这次竞赛中，成绩高于60分的学生占总人数的百分比.

（4）成绩落在哪个范围内的人数最多？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在底面是菱形的四棱锥中, 平面，，点分别为的中点，设直线与平面交于点.

（1）已知平面平面，求证： .

（2）求直线与平面所成角的正弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】物联网（Internet of Things，缩写：IOT）是基于互联网、传统电信网等信息承载体，让所有能行使独立功能的普通物体实现互联互通的网络. 其应用领域主要包括运输和物流、工业制造、健康医疗、智能环境（家庭、办公、工厂）等，具有十分广阔的市场前景. 现有一家物流公司计划租地建造仓库储存货物，经过市场调查了解到下列信息：仓库每月土地占地费（单位：万元），仓库到车站的距离（单位：千米，），其中与成反比，每月库存货物费（单位：万元）与成正比;若在距离车站9千米处建仓库，则和分别为2万元和7. 2万元. 这家公司应该把仓库建在距离车站多少千米处，才能使两项费用之和最小？最小费用是多少？