
【题目】已知 ![]() ,x∈R,且f(x)为奇函数. (I)求a的值及f(x)的解析式;
,x∈R,且f(x)为奇函数. (I)求a的值及f(x)的解析式;
(II)判断函数f(x)的单调性.
科目:高中数学 来源: 题型:
【题目】第十二届全国人名代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(1)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
(2)根据题意建立![]() 列联表,并判断是否有99%的把握认为男生与女生对两会的关注有差异?
列联表,并判断是否有99%的把握认为男生与女生对两会的关注有差异?
附:  ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为F,右顶点为A,设离心率为e,且满足
的右焦点为F,右顶点为A,设离心率为e,且满足![]() ,其中O为坐标原点.
,其中O为坐标原点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点![]() 的直线l与椭圆交于M,N两点,求△OMN面积的最大值.
的直线l与椭圆交于M,N两点,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
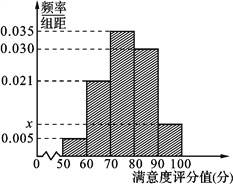
(1) 求图中![]() 的值;
的值;
(2) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,直线y=x+2过椭圆C的左焦点F1.
,直线y=x+2过椭圆C的左焦点F1.
(1)求椭圆C的标准方程;
(2)设过点A(0,﹣1)的直线l与椭圆交于不同两点M、N,当△MON的面积为![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:已知函数f(x)在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数f(x)在[m,n](m<n)上具有“DK”性质.例如函数 ![]() 在[1,9]上就具有“DK”性质.
在[1,9]上就具有“DK”性质.
(1)判断函数f(x)=x2﹣2x+2在[1,2]上是否具有“DK”性质?说明理由;
(2)若g(x)=x2﹣ax+2在[a,a+1]上具有“DK”性质,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com