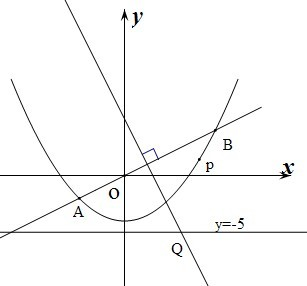
分析:(1)由抛物线x
2=8y得:其准线为y=-2,焦点为(0,2),根据点M(x
0,y
0)(x
0>0)是抛物线上到焦点距离为4的点,可得M到准线距离为4,从而可知M的纵坐标为2,代入抛物线x
2=8y方程知横坐标为4,从而可求点M的坐标;
(2)由直线
y=x+4与抛物线x
2=8y得点A、B坐标分别为(-4,2)(8,8).由于M和A关于y轴对称,所以可设△ABM的外接圆方程为x
2+(y-b)
2=r
2,代入A、B 两点坐标得
,从而可求△ABM的外接圆方程.
解答:解:(1)由抛物线x
2=8y得:其准线为y=-2,焦点为(0,2)
∵点M(x
0,y
0)(x
0>0)是抛物线上到焦点距离为4的点
∴M到准线距离为4,
∴M的纵坐标为2,代入抛物线x
2=8y方程知横坐标为4,
故点M的坐标为(4,2)
(2)由直线
y=x+4与抛物线x
2=8y得点A、B坐标分别为(-4,2)(8,8).
由于M和A关于y轴对称,所以可设△ABM的外接圆方程为x
2+(y-b)
2=r
2,
代入A、B 两点坐标得
∴b=9,r
2=65,
所以△ABM的外接圆方程为x
2+(y-9)
2=65
点评:本题以抛物线方程为载体,考查抛物线的定义,考查三角形外接圆的求解,解题的关键是正确运用抛物线的定义.



 阅读快车系列答案
阅读快车系列答案