练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知95个数a1，a2，a3，…，a95， 则a1a2+a1a3+…+a94a95的最小正值是______________．

    【答案】13

    【解析】根据题意,令t= a1a2+a1a3+…+a94a95

    则2t=2(a1a2+a1a3+…+a94a95)=(a1+a2+…+a95)2(a12+a22+…+a952)，

    又由a1,a2,…,a95每个都只能取+1或1两个值之一,则a12+a22+…+a952=95

    即2t=(a1+a2+…+a95)295，

    要使t取最小正数,t中(a1+a2+…+a95)2大于95即可，

    而a1+a2+…+a95为奇数个1、1的和，不会得偶数，

    则要使所求值取最小正数,须使(a1+a2+…+a95)=±11，

    因此t的最小值为.

    故答案为：13.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （1）当时，求的单调区间；

    （2）当时，若存在使得成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来许多地市空气污染较为严重，现随机抽取某市一年（365天）内100天的空气质量指数（）的监测数据，统计结果如表：

    指数

    空气质量

    优

    良

    轻度污染

    中度污染

    重度污染

    严重污染

    天数

    4

    13

    18

    30

    20

    15

    记某企业每天由空气污染造成的经济损失为（单位：元），指数为.当在区间内时，对企业没有造成经济损失；当在区间内时，对企业造成的经济损失与成直线模型（当指数为150时，造成的经济损失为1100元，当指数为200时，造成的经济损失为1400元）；当指数大于300时，造成的经济损失为2000元.　

    （1）试写出的表达式；

    （2）试估计在本年内随机抽取1天，该天经济损失大于1100且不超过1700元的概率；

    （3）若本次抽取的样本数据有30天是在供暖季，这30天中有8天为严重污染，完成列联表，并判断是否有的把握认为该市本年度空气严重污染与供暖有关？

    非严重污染

    严重污染

    合计

    供暖季

    非供暖季

    合计

    附：

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

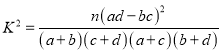    ，其中

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （Ⅰ）求曲线在处的切线方程．

    （Ⅱ）求的单调区间．

    （Ⅲ）设，其中，证明：函数仅有一个零点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中

    （Ⅰ）若函数存在相同的零点，求的值；

    （Ⅱ）若存在两个正整数，当时，有与同时成立，求的最大值及取最大值时的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)求函数的单调区间;

    (2)当时,函数的图象恒不在轴的上方,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足： ， ， .　

    （1）证明： ；

    （2）证明： ；

    （3）证明： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中， ， ，点M是线段AB上的一点，且．

    （1）证明：平面平面ABCD；

    （2）求直线CM与平面PCD所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】要分析学生初中升学考试的数学成绩对高一年级数学学习有什么影响，在高一年级学生中随机抽取10名学生，分析他们入学的数学成绩(x)和高一年级期末数学考试成绩(y)(如下表)：

    (1)画出散点图；

    (2)判断入学成绩(x)与高一期末考试成绩(y)是否有线性相关关系；

    (3)如果x与y具有线性相关关系，求出回归直线方程；

    编号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    x

    63

    67

    45

    88

    81

    71

    52

    99

    58

    76

    y

    65

    78

    52

    85

    92

    89

    73

    98

    56

    75

    查看答案和解析>>

    同步练习册答案