
【题目】已知函数 ![]() 在
在 ![]() 上有最大值1和最小值0,设
上有最大值1和最小值0,设 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)若不等式 ![]() 在
在 ![]() 上有解,求实数
上有解,求实数 ![]() 的取值范围;
的取值范围;
(3)若方程 ![]() (
( ![]() 为自然对数的底数)有三个不同的实数解,求实数
为自然对数的底数)有三个不同的实数解,求实数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解: ![]() ,当
,当 ![]() 时,
时, ![]() 在
在 ![]() 上是增函数,∴
上是增函数,∴ ![]() ,
,
即 ![]() ,解得
,解得 ![]() ,
,
当 ![]() 时,
时, ![]() ,无最大值和最小值;
,无最大值和最小值;
当 ![]() 时,
时, ![]() 在
在 ![]() 上是减函数,∴
上是减函数,∴ ![]() ,即
,即 ![]() ,解得
,解得 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() 舍去.
舍去.
综上, ![]() 的值分别为1、0
的值分别为1、0
(2)解:由(1)知 ![]() ,∴
,∴ ![]() 在
在 ![]() 上有解等价于
上有解等价于
![]() 在
在 ![]() 上有解,
上有解,
即 ![]() 在
在 ![]() 上有解,令
上有解,令 ![]() ,则
,则 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,记
,记 ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() 的取值范围为
的取值范围为 ![]()
(3)解:原方程可化为 ![]() ,令
,令 ![]() ,则
,则 ![]() ,
,
由题意知 ![]() 有两个不同的实数解
有两个不同的实数解 ![]() ,
, ![]() ,
,
其中 ![]() ,
, ![]() 或
或 ![]() ,
, ![]() ,
,
记 ![]() ,则
,则 ![]() 得
得 ![]()
【解析】(1)根据m的取值不同讨论函数g(x)的单调性,从而确定函数的最大值和最小值,列出方程组即可求解;(2)原不等式等价于![]() +
+![]()
![]() 2k
2k![]() 在[2,4]上有解,即2k
在[2,4]上有解,即2k![]()
![]()
![]() +1在[2,4]上有解,令t=
+1在[2,4]上有解,令t=![]() ,构造函数
,构造函数![]() (t)=t2-2t+1,并求出该函数在[
(t)=t2-2t+1,并求出该函数在[![]() ,1]上的最大值,进而可求出k的取值范围;(3)将原方程化简,令q=
,1]上的最大值,进而可求出k的取值范围;(3)将原方程化简,令q=![]() ,构造函数h(q)=q2-(3a+2)q+2a+1.
,构造函数h(q)=q2-(3a+2)q+2a+1.


科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米. (Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】)已知命题p:“x∈[1,2],x2﹣a≥0”,命题q:“x∈R,x2+2ax+2﹣a=0”.若命题“p且q”是真命题,则实数a的取值范围为( )
A.﹣2≤a≤1
B.a≤﹣2或1≤a≤2
C.a≥1
D.a≤﹣2或 a=1
查看答案和解析>>
科目:高中数学 来源: 题型:
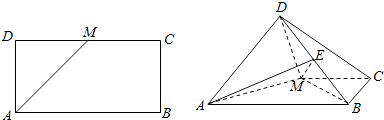
【题目】如图,已知长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
(Ⅱ)若点E是线段DB上的一动点,问点E在何位置时,二面角E﹣AM﹣D的余弦值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( ) 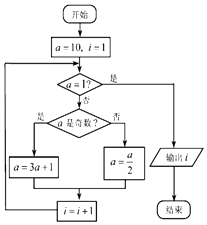
A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com