
【题目】某公司研发出一款新产品,批量生产前先同时在甲、乙两城市销售30天进行市场调查.调查结果发现:甲城市的日销售量![]() 与天数
与天数![]() 的对应关系服从图①所示的函数关系;乙城市的日销售量
的对应关系服从图①所示的函数关系;乙城市的日销售量![]() 与天数
与天数![]() 的对应关系服从图②所示的函数关系;每件产品的销售利润
的对应关系服从图②所示的函数关系;每件产品的销售利润![]() 与天数
与天数![]() 的对应关系服从图③所示的函数关系,图①是抛物线的一部分.
的对应关系服从图③所示的函数关系,图①是抛物线的一部分.
图① ,图②
,图② ,图③
,图③
(1)设该产品的销售时间为![]() ,日销售利润为
,日销售利润为![]() ,求
,求![]() 的解析式;
的解析式;
(2)若在30天的销售中,日销售利润至少有一天超过2万元,则可以投入批量生产,该产品是否可以投入批量生产,请说明理由.
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程![]() (
(![]() 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线 l 的极坐标方程是 ![]() ,射线OM:
,射线OM:![]() 与圆C的交点为O、P,与直线 l 的交点为Q,求线段PQ的长.
与圆C的交点为O、P,与直线 l 的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.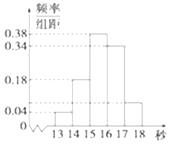
(1)设m,n表示样本中两个学生的百米测试成绩,已知m,n∈[13,14)∪[17,18],求事件“|m-n|>2”的概率;
(2)根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如附表:
根据上表数据,能否在犯错误的概率不超过0.01的前提下认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
附: 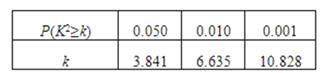
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生进行了三次数学测试,第一次有8名学生得满分,第二次有10名学生得满分,第三次有12名学生得满分,已知前两次均为满分的学生有5名,三次测试中至少有一次得满分的学生有15名,若后两次均为满分的学生至少有![]() 名,则
名,则![]() 的值为( )
的值为( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一条河的两岸平行,河的宽度d=600m,一艘客船从码头A出发匀速驶往河对岸的码头B.已知|AB|=1km,水流速度为2km/h, 若客船行驶完航程所用最短时间为6分钟,则客船在静水中的速度大小为( )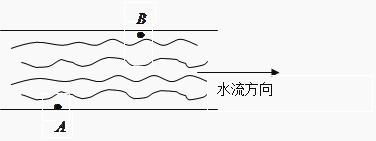
A.8km/h
B.![]() km/h
km/h
C.![]() km/h
km/h
D.10km/h
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在R上的偶函数,对于x∈R,都有f(x+4)=f(x)+f(2)成立,当x1,x2∈[0,2]且x1≠x2时,都有![]() 给出下列四个命题:
给出下列四个命题:
①f(﹣2)=0;
②直线x=﹣4是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[4,6]上为减函数;
④函数y=f(x)在(﹣8,6]上有四个零点.
其中所有正确命题的序号为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com