
【题目】![]() 中有:①若
中有:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() —定为等腰三角形;③若
—定为等腰三角形;③若![]() ,则
,则![]() —定为直角三角形;④若
—定为直角三角形;④若![]() ,且该三角形有两解,则
,且该三角形有两解,则![]() 的范围是
的范围是![]() .以上结论中正确的个数有( )
.以上结论中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
①根据正弦定理可得到结果;②根据![]() 或
或![]() 可得到结论不正确;③可由余弦定理推得
可得到结论不正确;③可由余弦定理推得![]() ,三角形为直角三角形; ④根据正弦定理得到:sinC=
,三角形为直角三角形; ④根据正弦定理得到:sinC=![]() ,由题意得:当C∈(90°,120°)时,满足条件的△ABC有两个,所以:
,由题意得:当C∈(90°,120°)时,满足条件的△ABC有两个,所以:![]() ,进而得到b的范围.
,进而得到b的范围.
①根据大角对大边得到a>b,再由正弦定理![]() 知
知![]() ①正确;②
①正确;②![]() ,则
,则![]() 或
或![]()
![]() 是直角三角形或等腰三角形;所以②错误;③由已知及余弦定理可得
是直角三角形或等腰三角形;所以②错误;③由已知及余弦定理可得![]() ,化简得
,化简得![]() ,所以③正确;④在△ABC中,∵B=60°,c=2,若满足条件的三角形恰有两个,
,所以③正确;④在△ABC中,∵B=60°,c=2,若满足条件的三角形恰有两个,
由正弦定理得:![]() 变形得:sinC=
变形得:sinC=![]() ,由题意得:当C∈(90°,120°)时,满足条件的△ABC有两个,所以:
,由题意得:当C∈(90°,120°)时,满足条件的△ABC有两个,所以:![]() ,解得:
,解得:![]() <b<2,则b的取值范围是(
<b<2,则b的取值范围是(![]() ,2).故④错误.
,2).故④错误.
故答案为:B.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮饮料销售的影响.经过统计,得到一个卖出的热饮杯数与当天气温的散点图和对比表

摄氏温度 | —5 | 4 | 7 | 10 | 15 | 23 | 30 | 36 |
热饮杯数 | 162 | 128 | 115 | 135 | 89 | 71 | 63 | 37 |
(参考公式) ,
,
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() .样本中心点为
.样本中心点为![]() .
.
(1)从散点图可以发现,各点散布在从左上角到右下角的区域里.因此,气温与当天热饮销售杯数之间成负相关,即气温越高,当天卖出去的热饮杯数越少.统计中常用相关系数![]() 来衡量两个变量之间线性关系的强弱.统计学认为,对于变量
来衡量两个变量之间线性关系的强弱.统计学认为,对于变量![]() 、
、![]() ,如果
,如果![]() ,那么负相关很强;如果
,那么负相关很强;如果![]() ,那么正相关很强;如果
,那么正相关很强;如果![]() ,那么相关性一般;如果
,那么相关性一般;如果![]() ,那么相关性较弱.请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
,那么相关性较弱.请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
(2)(i)请根据已知数据求出气温与当天热饮销售杯数的线性回归方程;
(ii)记![]() 为不超过
为不超过![]() 的最大整数,如
的最大整数,如![]() ,
,![]() .对于(1)中求出的线性回归方程
.对于(1)中求出的线性回归方程![]() ,将
,将![]() 视为气温与当天热饮销售杯数的函数关系.已知气温
视为气温与当天热饮销售杯数的函数关系.已知气温![]() 与当天热饮每杯的销售利润
与当天热饮每杯的销售利润![]() 的关系是
的关系是![]() (单位:元),请问当气温
(单位:元),请问当气温![]() 为多少时,当天的热饮销售利润总额最大?
为多少时,当天的热饮销售利润总额最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查;②运动会的工作人员为参加![]() 接力赛的6支队伍安排跑道;③一次数学月考中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人有解有关情况.针对这三个事件,恰当的抽样方法分别为( )
接力赛的6支队伍安排跑道;③一次数学月考中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人有解有关情况.针对这三个事件,恰当的抽样方法分别为( )
A.分层抽样、分层抽样、简单随机抽样B.系统抽样、简单随机抽样、分层抽样
C.简单随机抽样、简单随机抽样、分层抽样D.系统抽样、分层抽样、简单随机抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() :
:![]() =0(a>0),曲线
=0(a>0),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系;
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系;
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)已知极坐标方程为![]() =
=![]() 的直线与曲线
的直线与曲线![]() ,
,![]() 分别相交于P,Q两点(均异于原点O),若|PQ|=
分别相交于P,Q两点(均异于原点O),若|PQ|=![]() ﹣1,求实数a的值;
﹣1,求实数a的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数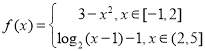 .
.
(1)在直角坐标系内直接画出![]() 的图象;
的图象;
(2)写出![]() 的单调区间,并指出单调性(不要求证明);
的单调区间,并指出单调性(不要求证明);
(3)若函数![]() 有两个不同的零点,求实数
有两个不同的零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有![]() ,
,![]() ,
,![]() ,
,![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
甲说:“![]() 、
、![]() 同时获奖”;
同时获奖”;
乙说:“![]() 、
、![]() 不可能同时获奖”;
不可能同时获奖”;
丙说:“![]() 获奖”;
获奖”;
丁说:“![]() 、
、![]() 至少一件获奖”.
至少一件获奖”.
如果以上四位同学中有且只有二位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“节能减排,绿色生态”为当今世界各国所倡导,某公司在科研部门的鼎力支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该公 司每月的处理量![]() (吨)至少为50吨,至多为220吨.月处理成本
(吨)至少为50吨,至多为220吨.月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系式近似表示为:
(吨)之间的函数关系式近似表示为:![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为120元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为120元.
(1)该公司每月处理量为多少吨时,才能使每吨的平均处理成本![]() 最低?
最低?
(2)每月处理量为多少吨时,月获利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com