
分析 运用等差(比)数列的定义分别求得${a}_{{k}_{n}}$,然后列方程求得kn.
解答 解:设{an}的首项为a1,
∵${a}_{{k}_{1}}$,${a}_{{k}_{2}}$,${a}_{{k}_{3}}$成等比数列,
∴(a1+4d)2=a1(a1+16d).
得a1=2d,q=$\frac{{a}_{{k}_{2}}}{{a}_{{k}_{1}}}$=3.
∵${a}_{{k}_{n}}$=a1+(kn-1)d,又${a}_{{k}_{n}}$=a1•3n-1,
∴kn=2•3n-1-1.
故答案为:2•3n-1-1.
点评 运用等差(比)数列的定义转化为关于kn的方程是解题的关键,转化时要注意:akn是等差数列中的第kn项,而是等比数列中的第n项,是中档题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6.5 h | B. | 5.5 h | C. | 3.5 h | D. | 0.5 h |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-∞,1] | C. | (1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
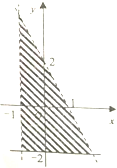
| A. | $\left\{\begin{array}{l}{x+1>0}\\{2x+y<2}\\{y≥-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1≥0}\\{2x+y≤2}\\{y>-2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+1≥0}\\{2x+y<2}\\{y>-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+1<0}\\{2x+y<2}\\{y>-2}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com