
【题目】如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=3,AB=![]() ,BE=
,BE=![]() EC,AD=2DC.
EC,AD=2DC.

(1)证明:DE⊥平面PAE;
(2)求二面角A-PE-B的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先证明AB, AC, AP两两垂直,然后以点A为原点建立空间直角坐标系,证明![]() =0,
=0,![]() ,从而得到DE⊥AE,DE⊥AP,故得结论成立.(2)由题意求得平面PEB的法向量
,从而得到DE⊥AE,DE⊥AP,故得结论成立.(2)由题意求得平面PEB的法向量![]() ,又由(1)得
,又由(1)得![]() =(1,-1,0)是平面APE的一个法向量,求出
=(1,-1,0)是平面APE的一个法向量,求出![]() 后再结合图形得到所求的余弦值.
后再结合图形得到所求的余弦值.
(1)证明:
∵PA⊥平面ABC, AB, AC在平面ABC内,
∴PA⊥AB,PA⊥AC.
又AB⊥AC,
∴AB, AC, AP两两垂直,
以点A为坐标原点,AB,AC,AP分别为x,y,z轴建立如图所示的空间直角坐标系,
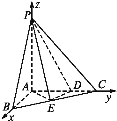
由题意得A(0,0,0),B![]() ,C(0,3,0),P(0,0,3),
,C(0,3,0),P(0,0,3),
∵BE=![]() EC,
EC,
∴E(1,1,0).
∵AD=2DC,
∴D(0,2,0).
∴![]() =(1,-1,0),
=(1,-1,0),![]() =(1,1,0).
=(1,1,0).
∵![]() =0,
=0,
∴![]() ,
,
∴DE⊥AE,
同理可得DE⊥AP,
又AP∩AE=A,
∴DE⊥平面PAE.
(2)解设![]() 是平面PEB的一个法向量,
是平面PEB的一个法向量,
则
令z=1,则![]() ,
,
由(1)得![]() =(1,-1,0)是平面APE的一个法向量,
=(1,-1,0)是平面APE的一个法向量,
∴cos<![]() ,
,![]() >=
>=![]() ,
,
由图形得二面角A-PE-B为锐角,
∴二面角A-PE-B的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列语句中是命题的有________,其中是真命题的有_____(填序号).
①“垂直于同一条直线的两个平面必平行吗?”②“一个数不是正数就是负数”;③“在一个三角形中,大角所对的边大于小角所对的边”;④“若x+y为有理数,则x,y都是有理数”;⑤作一个三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ ![]() ax2﹣2x,其中a≤0.
ax2﹣2x,其中a≤0.
(1)若曲线y=f(x)在点(1,f(1))处的切线方程为y=2x+b,求a﹣2b的值;
(2)讨论函数f(x)的单调性;
(3)设函数g(x)=x2﹣3x+3,如果对于任意的x,t∈(0,1],都有f(x)≤g(t)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C所对边的边长,且C=![]() ,a+b=λc(其中λ>1).
,a+b=λc(其中λ>1).
(1)若λ=![]() 时,证明:△ABC为直角三角形;
时,证明:△ABC为直角三角形;
(2)若![]() ·
·![]() =
=![]() λ2,且c=3,求λ的值.
λ2,且c=3,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(I)已知函数f(x)=rx﹣xr+(1﹣r)(x>0),其中r为有理数,且0<r<1.求f(x)的最小值;
(II)试用(I)的结果证明如下命题:设a1≥0,a2≥0,b1 , b2为正有理数,若b1+b2=1,则a1b1a2b2≤a1b1+a2b2;
(III)请将(II)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题.注:当α为正有理数时,有求导公式(xα)r=αxα﹣1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(1)求A;
(2)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的导函数y=f'(x)的图像如图所示.

则下列说法中正确的是____(填序号).
①函数y=f(x)在区间![]() 上单调递增;
上单调递增;
②函数y=f(x)在区间![]() 上单调递减;
上单调递减;
③函数y=f(x)在区间(4,5)上单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x=-![]() 时,函数y=f(x)有极大值.
时,函数y=f(x)有极大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{an}的前n项和,已知a1≠0,2an﹣a1=S1Sn , n∈N* .
(1)求a1a2 , 并求数列{an}的通项公式,
(2)求数列{nan}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
项目 | 男性 | 女性 | 总计 |
反感 | 10 | ||
不反感 | 8 | ||
总计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是![]() .
.
(1)请将上面的列联表补充完整(直接写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
附:K2=![]()
.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com