
【题目】设数列{an}的前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N*.
(1)求a1的值;
(2)求数列{an}的通项公式.
【答案】
(1)解: 由题意a1=S1=T1,Tn=2Sn-n2,
令n=1得a1=2a1-1,∴a1=1.
(2)解: 由Tn=2Sn-n2①
得Tn-1=2Sn-1-(n-1)2(n≥2)②
①-②得Sn=2an-2n+1(n≥2),
验证n=1时也成立.
∴Sn=2an-2n+1③
则Sn-1=2an-1-2(n-1)+1(n≥2)④
③-④得an=2an-2an-1-2,
即an+2=2(an-1+2),
故数列{an+2}是公比为2的等比数列,首项为3,
所以an+2=3·2n-1,从而an=3·2n-1-2.
【解析】(1)根据T1=S1=a1即可求出a1;(2)根据Sn=![]() 得到Sn与an的关系式,再根据an=
得到Sn与an的关系式,再根据an=![]() 得到an与an-1的关系式,利用待定系数法构造特殊数列即可求解.
得到an与an-1的关系式,利用待定系数法构造特殊数列即可求解.
【考点精析】根据题目的已知条件,利用数列的通项公式的相关知识可以得到问题的答案,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】函数y=f(x)是定义域为R的偶函数,且在(0,+∞)上单调递减,则( )
A.f(﹣π)>f(﹣1)>f( ![]() )
)
B.f(﹣1)>f(﹣π)>f( ![]() )
)
C.f(﹣π)>f( ![]() )>f(﹣1)
)>f(﹣1)
D.f(﹣1)>f( ![]() )>f(﹣π)
)>f(﹣π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?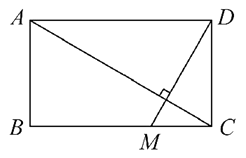
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.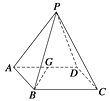
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}及等差数列{bn},若a1=3, ![]() (n≥2),a1=b2 , 2a3+a2=b4 ,
(n≥2),a1=b2 , 2a3+a2=b4 ,
(1)证明数列{an﹣2}为等比数列;
(2)求数列{an}及数列{bn}的通项公式;
(3)设数列{anbn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】咖啡馆配制两种饮料,甲种饮料每杯分别用奶粉、咖啡、糖9g、4g、3g;乙种饮料每杯分别用奶粉、咖啡、糖4g、5g、10g,已知每天使用原料限额为奶粉3600g,咖啡2000g,糖3000g,如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料使用的限额内,饮料能全部售完,问咖啡馆每天怎样安排配制饮料获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系.已知曲线C1: ![]() (t为参数),C2:
(t为参数),C2: ![]() (θ为参数). (Ⅰ)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(θ为参数). (Ⅰ)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若C1上的点P对应的参数为t=﹣ ![]() ,Q为C2上的动点,求线段PQ的中点M到直线C3:ρcosθ﹣
,Q为C2上的动点,求线段PQ的中点M到直线C3:ρcosθ﹣ ![]() ρsinθ=8+2
ρsinθ=8+2 ![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com