
一个盒子中装有形状大小相同的5张卡片,上面分别标有数字1,2,3,4,5,甲乙两人分别从盒子中随机不放回的各抽取一张.
(Ⅰ)写出所有可能的结果,并求出甲乙所抽卡片上的数字之和为偶数的概率;
(Ⅱ)以盒子中剩下的三张卡片上的数字作为边长来构造三角形,求出能构成三角形的概率.
(Ⅰ)甲乙两人分别从盒子中随机不放回的各抽取一张,基本事件有
 共20个;
共20个; .
.
(Ⅱ) .
.
解析试题分析:(Ⅰ)借助于“树图法”可得基本事件有:
 共20个
共20个
设事件 “甲乙所抽卡片上的数字之和为偶数”
“甲乙所抽卡片上的数字之和为偶数”
其中甲乙所抽卡片上的数字之和为偶数的有: 共8个,利用概率计算公式计算.
共8个,利用概率计算公式计算.
(Ⅱ)剩下的三边长包含的基本事件为: 共10个;
共10个;
其中“剩下的三张卡片上的数字作为边长能构成三角形”的有: 共3个.
共3个.
解答此类问题,关键是计算正确“事件数”,“列表法”“树图法”“坐标法”等,是常用方法.
试题解析:(Ⅰ)甲乙两人分别从盒子中随机不放回的各抽取一张,基本事件有
 共20个 2分
共20个 2分
设事件 “甲乙所抽卡片上的数字之和为偶数”
“甲乙所抽卡片上的数字之和为偶数”
则事件 包含的基本事件有
包含的基本事件有 共8个 4分
共8个 4分
所以 . 6分
. 6分
(Ⅱ)剩下的三边长包含的基本事件为: 共10个; 8分
共10个; 8分
设事件 “剩下的三张卡片上的数字作为边长能构成三角形“
“剩下的三张卡片上的数字作为边长能构成三角形“
则事件 包含的基本事件有:
包含的基本事件有: 共3个 10分
共3个 10分
所以 . 12分
. 12分
备注:第二问也可看做20个基本事件,重复一倍。
考点:古典概型概率的计算


科目:高中数学 来源: 题型:解答题
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱)
(1)求在一次游戏中
①摸出3个白球的概率;②获奖的概率.
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以 表示.
表示.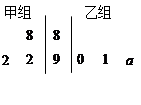
(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求 的值;
的值;
(Ⅱ)求乙组平均成绩超过甲组平均成绩的概率;
(Ⅲ)当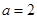 时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为
时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为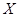 ,求随机变量
,求随机变量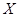 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示.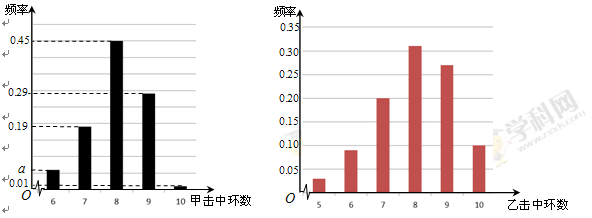
假设每名队员每次射击相互独立.
(Ⅰ)求上图中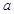 的值;
的值;
(Ⅱ)队员甲进行三次射击,求击中目标靶的环数不低于8环的次数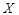 的分布列及数学期望(频率当作概率使用);
的分布列及数学期望(频率当作概率使用);
(Ⅲ)由上图判断,在甲、乙两名队员中,哪一名队员的射击成绩更稳定?(结论不需证明)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一次抢险救灾中,某救援队的50名队员被分别分派到四个不同的区域参加救援工作,其分布的情况如下表,从这50名队员中随机抽出2人去完成一项特殊任务.
| 区域 | A | B | C | D |
| 人数 | 20 | 10 | 5 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司计划在迎春节联欢会中设一项抽奖活动:在一个不透明的口袋中装入外形一样号码分别为1,2,3,…,10的十个小球。活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金。
(1)求员工甲抽奖一次所得奖金ξ的分布列与期望;
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数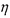 的方差是多少?
的方差是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了参加2013年东亚运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源如下表:
| 对别 | 北京 | 上海 | 天津 | 广州 |
| 人数 | 4 | 6 | 3 | 5 |
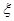 ,求随机变量
,求随机变量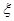 的分布列,及数学期望.
的分布列,及数学期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,从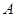 到
到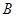 有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为
有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为 .
.
(1)当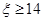 时,线路信息畅通,求线路信息畅通的概率;
时,线路信息畅通,求线路信息畅通的概率;
(2)求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
由于某高中建设了新校区,为了交通方便要用三辆通勤车从新校区把教师接到老校区,已知从新校区到老校区有两条公路,汽车走公路①堵车的概率为 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
(1)若三辆汽车中恰有一辆汽车被堵的概率为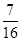 ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(2)在(1)的条件下,求三辆汽车中被堵车辆的个数ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com