
【题目】设椭圆![]() 长轴长为4,右焦点
长轴长为4,右焦点![]() 到左顶点的距离为3.
到左顶点的距离为3.
(1)求椭圆![]() 的方程;
的方程;
(2)设过原点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点(
两点(![]() 不在坐标轴上),连接
不在坐标轴上),连接![]() 并延长交椭圆于点
并延长交椭圆于点![]() ,若
,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知三棱柱![]() 平面
平面![]() 是
是![]() 内一点,点
内一点,点![]() 在直线
在直线![]() 上运动,若直线
上运动,若直线![]() 和
和![]() 所成角的最小值与直线
所成角的最小值与直线![]() 和平面
和平面![]() 所成角的最大值相等,则满足条件的点
所成角的最大值相等,则满足条件的点![]() 的轨迹是( )
的轨迹是( )
A.直线的一部分B.圆的一部分C.抛物线的一部分D.椭圆的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平行四边形ABCD中,∠A![]() ,2AB=BC,E,F分别是BC,AD的中点.将四边形DCEF沿着EF折起,使得平面ABEF⊥平面DCEF,得到三棱柱AFD﹣BEC.
,2AB=BC,E,F分别是BC,AD的中点.将四边形DCEF沿着EF折起,使得平面ABEF⊥平面DCEF,得到三棱柱AFD﹣BEC.
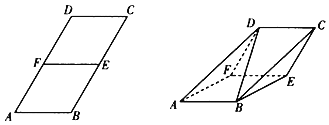
(1)证明:DB⊥EF;
(2)若AB=2,求三棱柱AFD﹣BEC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
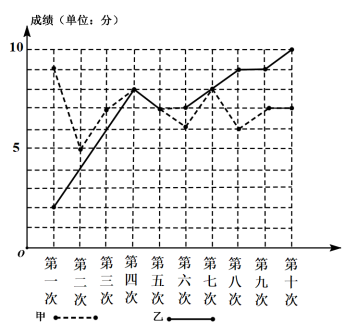
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系![]() 中,曲线
中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设
,设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 中点为
中点为![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() 、
、![]() .以
.以![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴的正半轴建立直角坐标系
轴的正半轴建立直角坐标系![]() .
.
(1)求![]() 的直角坐标方程与点
的直角坐标方程与点![]() 的直角坐标;
的直角坐标;
(2)求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com