
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,已知
,已知![]() ,求实数
,求实数![]() 的值.
的值.
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
【题目】记焦点在同一条轴上且离心率相同的椭圆为“相似椭圆”.已知椭圆![]() ,以椭圆
,以椭圆![]() 的顶点焦点为作相似椭圆
的顶点焦点为作相似椭圆![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且与椭圆
两点,且与椭圆![]() 仅有一个公共点,试判断
仅有一个公共点,试判断![]() 的面积是否为定值(
的面积是否为定值(![]() 为坐标原点)?若是,求出该定值;若不是,请说明理由.
为坐标原点)?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为改善人居环境,某区增加了对环境综合治理的资金投入,已知今年治理环境![]() (亩)与相应的资金投入
(亩)与相应的资金投入![]() (万元)的四组对应数据的散点图如图所示,用最小二乘法得到
(万元)的四组对应数据的散点图如图所示,用最小二乘法得到![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
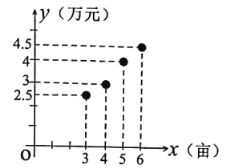
(1)求![]() 的值,并预测今年治理环境10亩所需投入的资金是多少万元?
的值,并预测今年治理环境10亩所需投入的资金是多少万元?
(2)已知该区去年治理环境10亩所投入的资金为3.5万元,根据(1)的结论,请你对该区环境治理给出一条简短的评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设直线![]() :
:![]() ,
,![]() :
:![]() .点
.点![]() 的坐标为
的坐标为![]() .过点
.过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,且与
,且与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() (
(![]() ,
,![]() 的纵坐标均为正数).
的纵坐标均为正数).
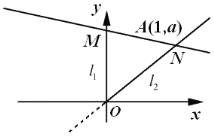
(1)求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,求
,求![]() 面积的最小值;
面积的最小值;
(3)是否存在实数![]() ,使得
,使得![]() 的值与
的值与![]() 无关?若存在,求出所有这样的实数
无关?若存在,求出所有这样的实数![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
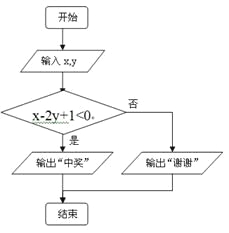
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com